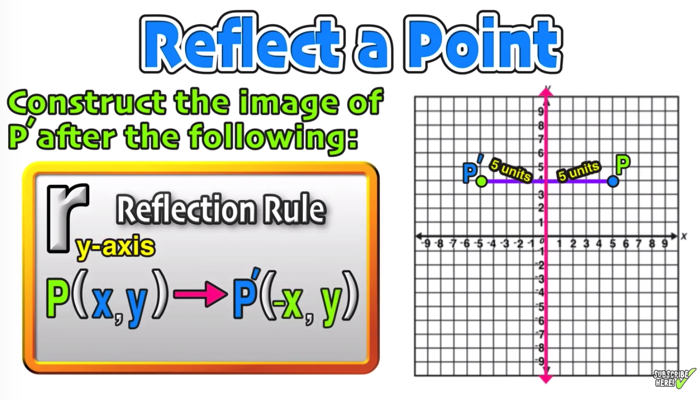
Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection A reflection of a point over the line y = − x y = −x is shownMay 24, 19 · In this lesson we'll look at how the reflection of a figure in a coordinate plane determines where it's located A reflection is a type of transformation that flips a figure over a line The line is called the line of reflection, or the mirror line The line of reflection can be horizontal, vertical, or diagonalUse our online point reflection calculator to know the point reflection for the given coordinates This calculator helps you to find the point reflection A, for the given coordinates of A (x,y) Just select an axis from the dropdown and enter the coordinates, the point reflection calculator will show the result Point reflection, also called as an inversion in a point is defined as an isometry

Reflection Mathbitsnotebook A1 Ccss Math
Y=x line reflection rule
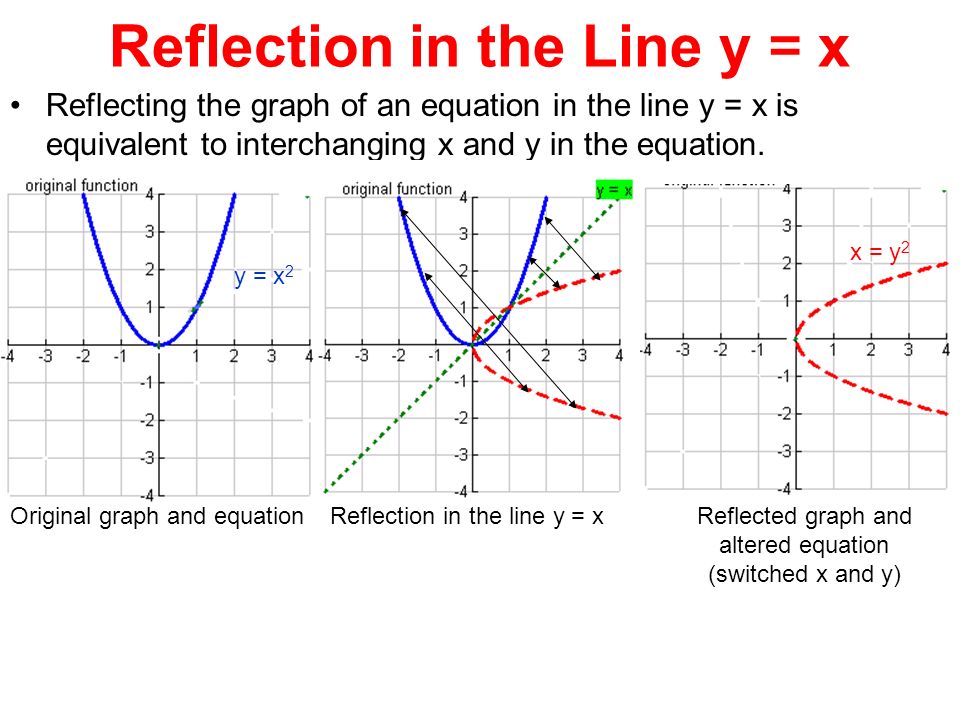
Y=x line reflection rule-May 07, · the line y = x is the point (y, x) Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure The line of reflection will lie directly in the middle between the original figure and its imageThe line segments connecting corresponding vertices will all be parallel to each other What is the preimage of vertex A' if the image shown on the graph was created by a reflection



Lesson On Line Of Reflection Y X
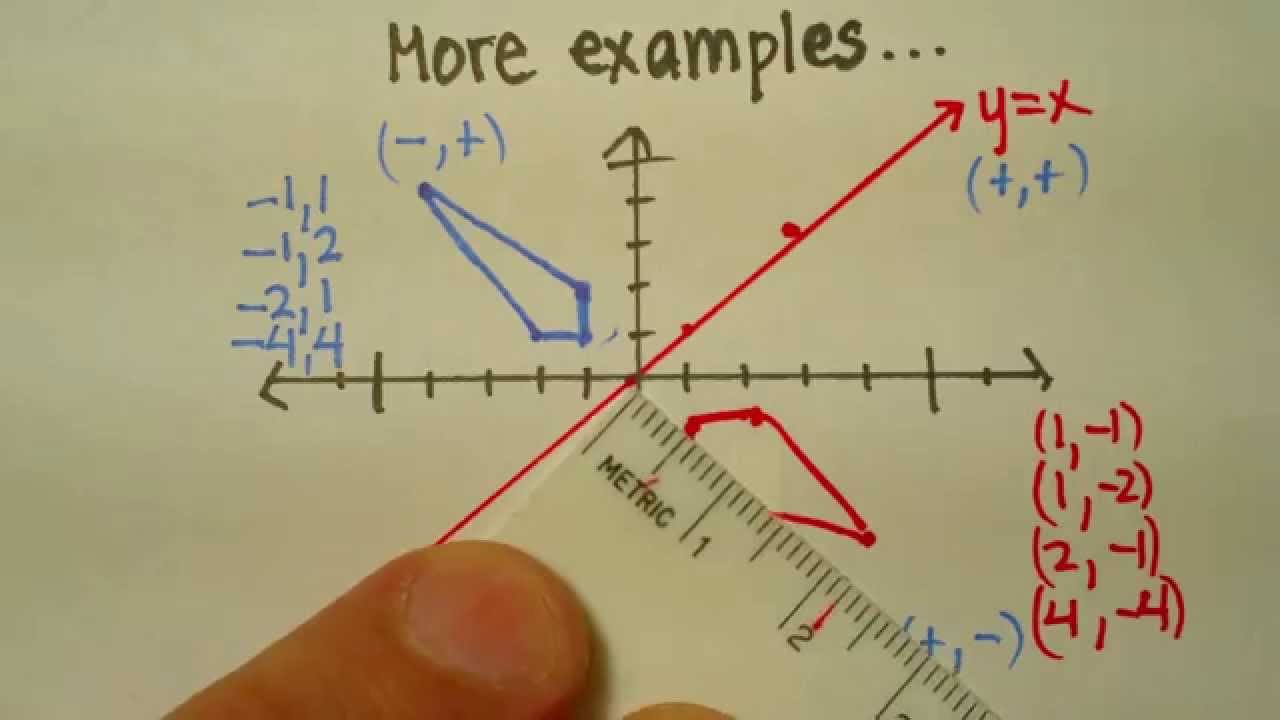
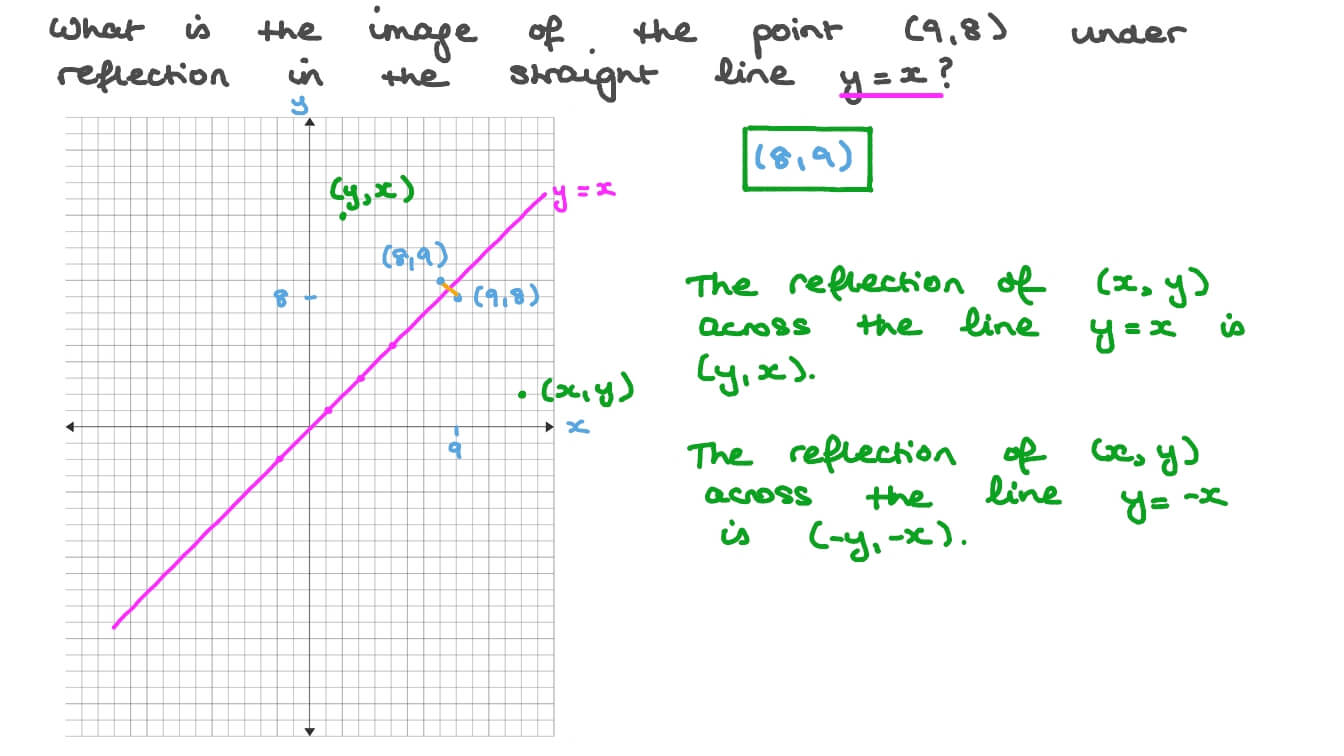
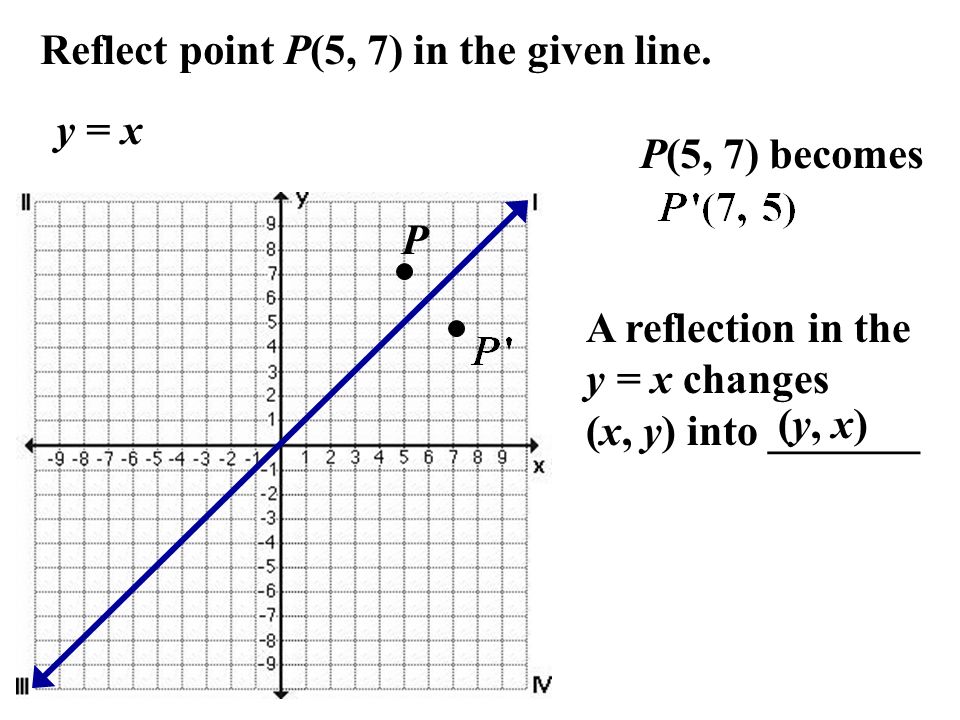
Dec 04, · When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places and are negated (the signs are changed) The reflection of the point (x, y) across the line y = x is the point (y, x) P(x,y)→P'(y,x) or r y=x (x,y) = (y,x) The reflection of the point (x, y) across the line y = x is the point (y, x)The resulting orientation of the two figures are opposite Corresponding parts of the figures are the same distance from the line of reflection Ordered pair rules reflect over the xaxis (x, y), yaxis (x, y), line y = x (y, x)What is a Reflection?
May 15, 21 · A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed;1) a line reflection over y =x 2) a rotation of 180° centered at (1,0) 3) a line reflection over the xaxis followed by a translation of 6 units right 4) a line reflection over the xaxis followed by a line reflection over y =1 4 In the diagram below, A′B′C′ is a transformation of ABC, and A″B″C″ is a transformation of A′B′C′Nov 13, 18 · ie (1,0) = (1,0) Therefore, the equation of the reflection of the line x = 1 in y axis is x1=0 ahlukileoi and 92 more users found this answer helpful
In this video, Michael and Paula take the graph \(y= 05x 1\) and reflect it in the line \(y = x\) to form the reflected image Michael and Paula explore what happens to coordinates on the object when reflected in the line y = x and then generalise their findingsLearn about reflection in mathematics every point is the same distance from a central lineTutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT


Diagonal Reflections In The Line Y X Teaching Resources



Reflection In The Line Y X Transformation Matrix Youtube
Reflection over some axis is a common mathematical transformation Generally, reflection is accomplished by changing the sign of something To reflect points across the line {eq}y=xReflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxisMay 10, 19 · A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y Axis



Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3


Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N
The line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I wiWe have reflected the shape in the line y = −x A Formula to Reflect a Point in y = −x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinatesWhen you look in the mirror, you see your reflection In math, you can create mirror images of figures by reflecting them over a given line This tutorial introduces you to reflections and shows you some examples of reflections Take a look!


Reflections



What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic
The reflection of the point (x, y) across the line y = – x is (y, x) Reflection in a Point A reflection point occurs when a figure is constructed around a single point known as the point of reflection or centre of the figure For every point in the figure, another point is found directly opposite to it on the other side Under the pointThe rule for a reflection in the line y = x is ( x , y ) → ( y , x ) Reflection in the line y = − x A reflection of a point over the line y = − x is shownReflections in the coordinate plane When you reflect a point across the xaxis, the xcoordinate remains the same, but the ycoordinate is transformed into its opposite (its sign is changed) If you forget the rules for reflections when graphing,



Reflection Over A Line Expii



The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange
A reflection (or flip) is one kind of transformation The reflection of a point is another point on the other side of a line of symmetry Both the point and its reflection are the same distance from the line The following diagram show the coordinate rules for reflection over the xaxis, yaxis, the line y = x and the line y = xReflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Hot Network Questions Under copyleft, why distinguish between "free as in free speech" and "free as in free beer"?



Reflection Rules How To W 25 Step By Step Examples


Transformation Matrix For Reflection In Y X Youtube
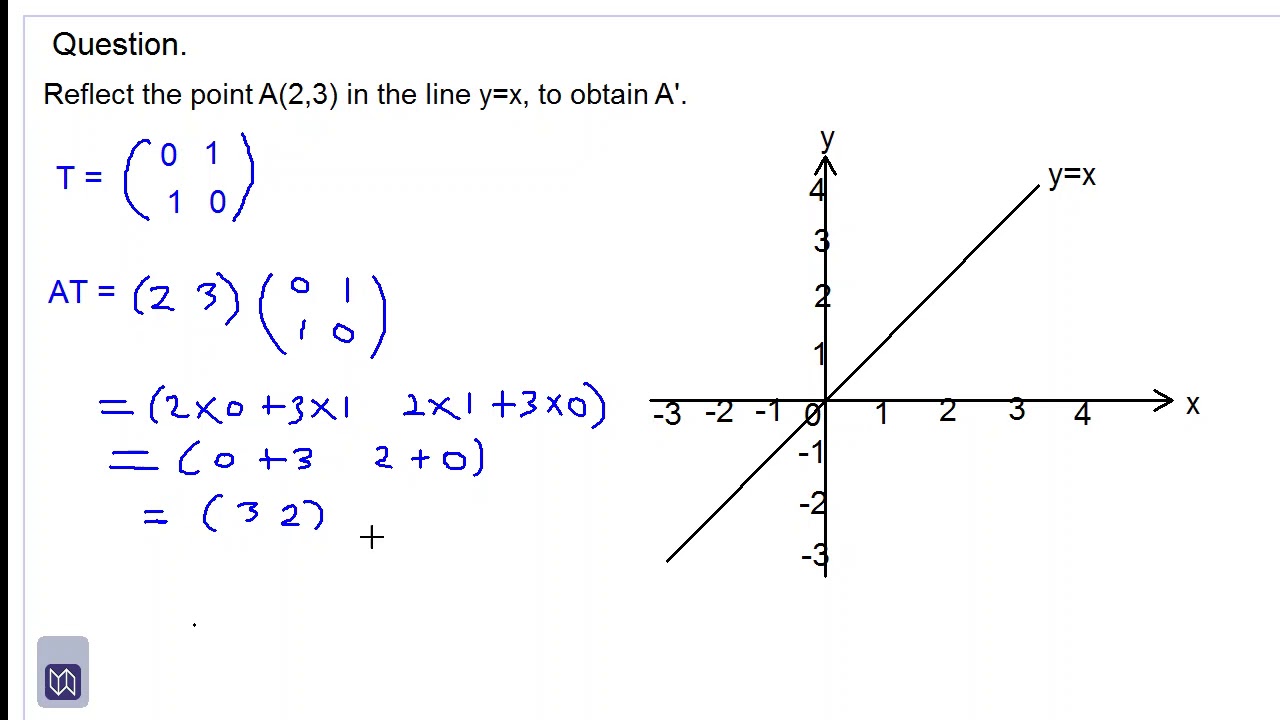
Feb 21, 11 · we've talked a lot about linear transformations what I want to do in this video and actually the next few videos is to show you how to essentially design linear transformations to do things to vectors that you want them to do so we already know that if I have some linear transformation T and it's a mapping from RN to R M that we can represent T what T does to anyThe resulting orientation of the two figures are opposite What are the 4 reflection rules?Step 1 First we have to write the vertices of the given triangle ABC in matrix form as given below Step 2 Since the triangle ABC is reflected about xaxis, to get the reflected image, we have to multiply the above matrix by the matrix given below Step 3



Reflection Over The Y X Line Youtube



How To Reflect A Graph Through The X Axis Y Axis Or Origin
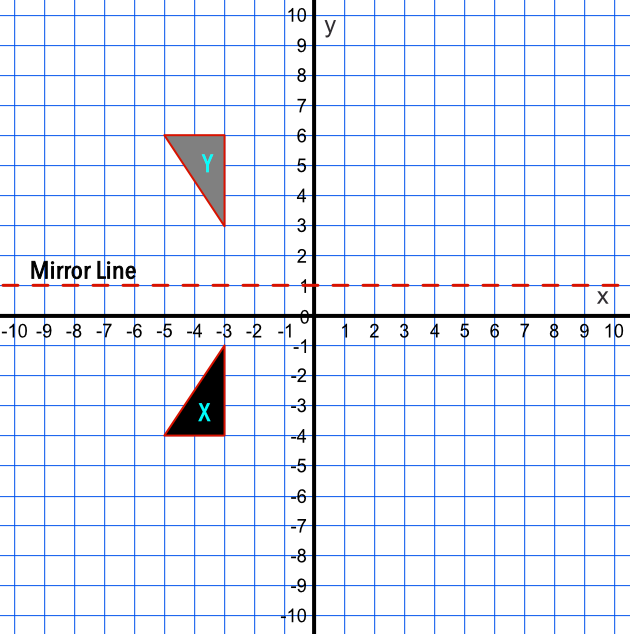
The equation of the line of the mirror line To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1In this series of tutorials I show you how we can apply matrices to transforming shapes by considering the transformations of two unit base vectors Reflections in the xaxis Reflections in the yaxis Reflection in the line y = x Reflection in the line y = xBackground Tutorials Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates



Reflection Mathbitsnotebook A1 Ccss Math



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
1 Reflection across the line y = x in 3 Dimensions?Reflection on a Coordinate Plane Reflection Over X AxisGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha



Performing Reflections Line Old Video Khan Academy



How Are We Studying Transformations Differently By Eureka Math Eureka Math Medium
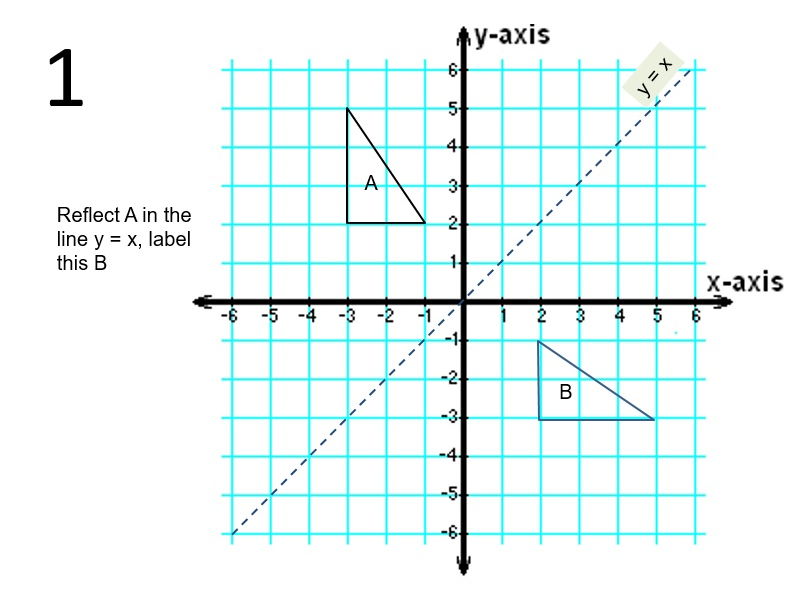
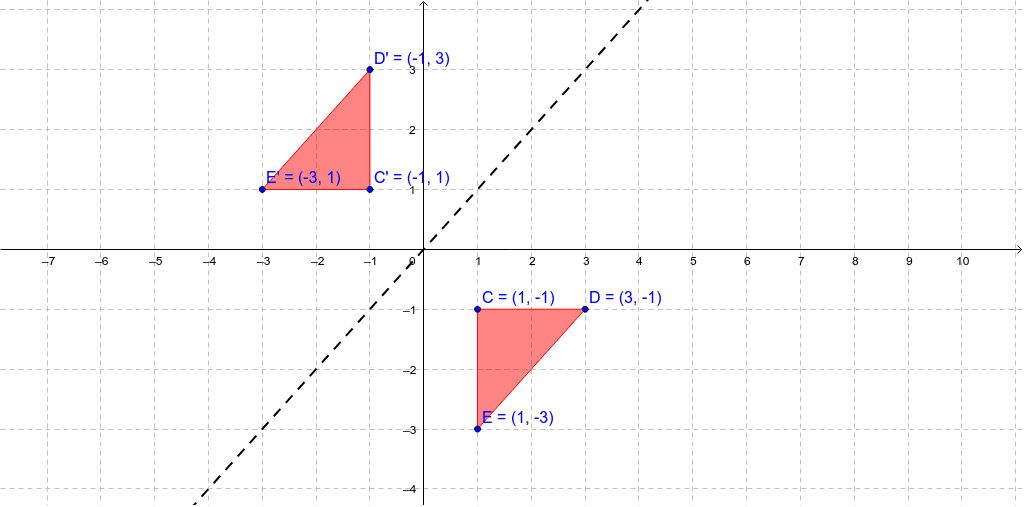
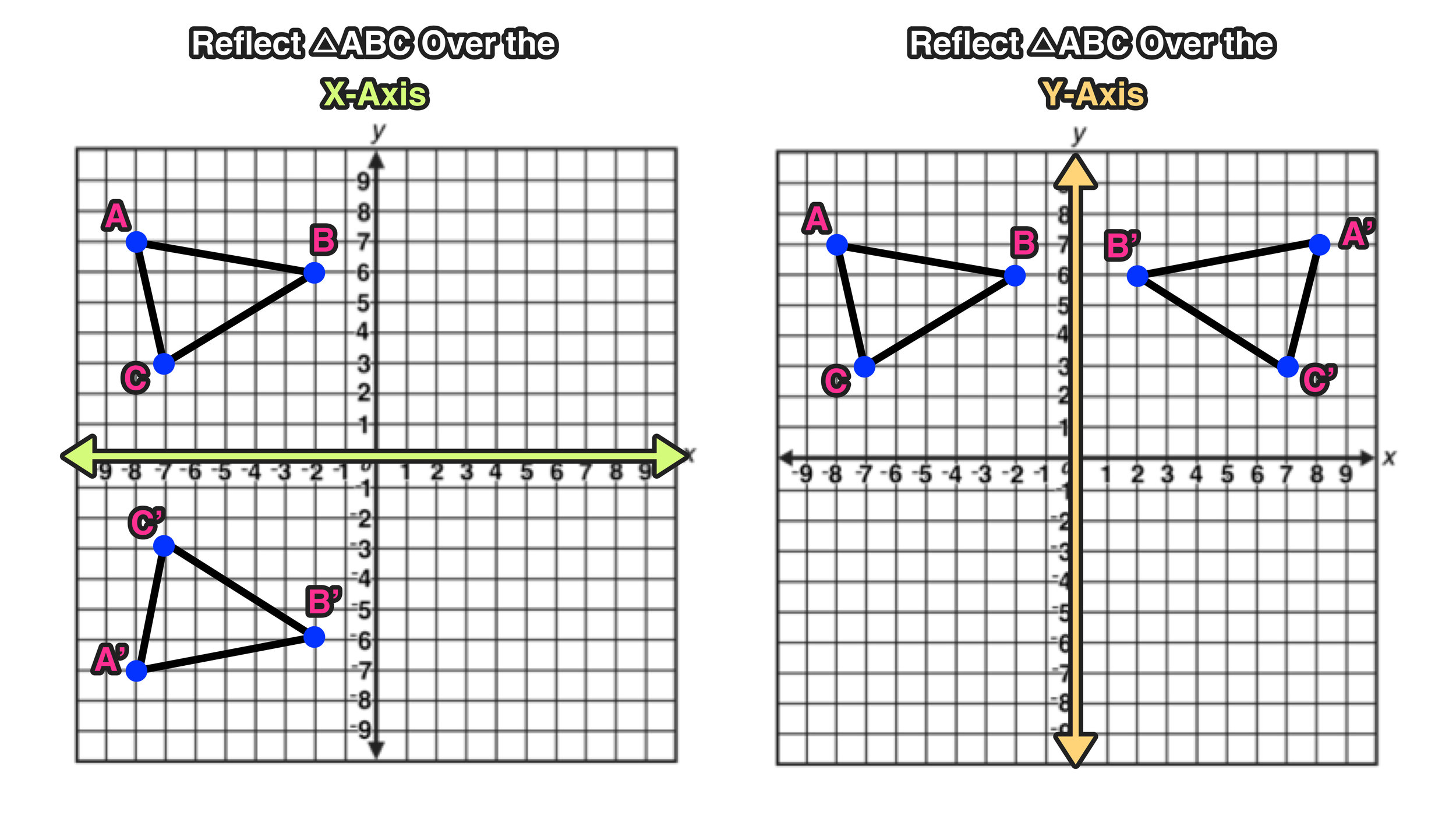
Sep 03, 18 · We have to identify the rules of reflection Firstly, the rule for reflecting a point about the line y=x is While reflecting about the line y=x, we get the reflected points by swapping the coordinates So, Option 3 is correct Now, the rule for reflecting a point about the line y= x is0 Linear transformation reflected across yaxis?A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3)



Rules For Reflections Read Geometry Ck 12 Foundation
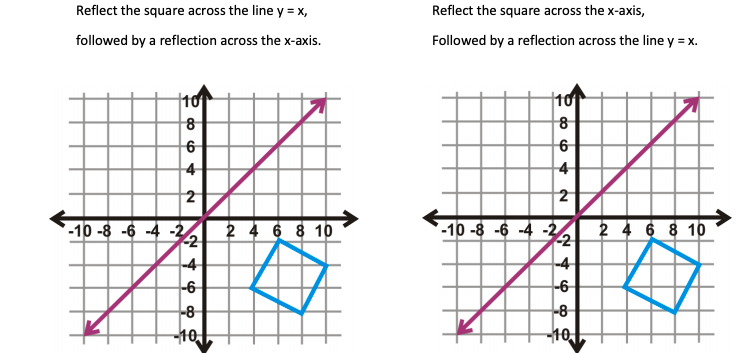


Solved Reflect The Square Across The Line Y X Followed Chegg Com
Graph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the yMar 29, · The lines y = x and y = x are the two primary diagonal lines of the coordinate plane and the most common diagonal lines over which points and shapes are reflected In a reflection over the line y = x, the x and ycoordinates simply switch positions For example, suppose the point (6, 7) is reflected over y = x How do you write a reflection?Flip over a line;



Reflection Transformation Matrix


Reflection Over The X And Y Axis The Complete Guide Mashup Math
ΔA'B'C' was constructed using ΔABC and line segment EH For to be the line of reflection between and , which statements must be true?Oct 13, 17 · You can use a formula When you reflect over xaxis the coordinates are (x,y) and when you reflect over the yaxis the coordinates are (x,y If you want to reflect over y=x then the coordinates are (y,x) If you want to reflect over y=x the coordinates are (y,x) Comment on Caylen Jang's post "You can use a formulaY = x, x‒axis, y = x, yaxis Triangle XYZ is shown on the coordinate plane belowIf triangle XYZ is reflected across the line y = 1 to create triangle X′Y′Z′, what is the ordered pair of X′?



What Is A Line Of Reflection Printable Summary Virtual Nerd



Reflection Over Y X Math Geometry Showme
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xJan 04, 21 · In some cases, the line of reflection may be on the edge – or even inside – the figure Three common ways to reflect figures are over the xaxis, yaxis, and the line y=x Something to notice as we look at these is that the signs of the coordinates change For example, when a figure is reflected over the xaxis, notice the ycoordinatesA reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = x (A, B) → (B, A)



Picture Of Reflection In The Line Y X Reflection Math Math Reflection


Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com
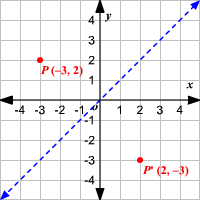
Reflection of a point across the line y = x The coordinate of point P is (2, 4) and the coordinate of the reflected image P' is (4, 2) The coordinate of point A is (4, 1) and the coordinate of the reflected image A' is (1, 4) Therefore, swap the xcoordinate with the ycoordinate and then take the opposite of both coordinatesWhat is the line of reflection of this 3x3 matrix?To perform a geometry reflection, a line of reflection is needed;


Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download



Learn About Reflection Over The Line Y X Caddell Prep Online



Algebraic Representations Of Reflections



Reflection Mathbitsnotebook A1 Ccss Math


Reflection In The Line Y X Geogebra



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines


Transformations Mathematics Gcse Revision


Reflection


Tbaisd Moodle



Reflections Through The Axes And The Lines Y X And Y X Geogebra



Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
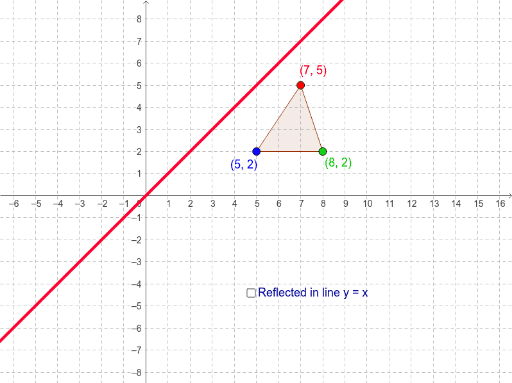


Reflection In The Line Y X Geogebra



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection Rules How To W 25 Step By Step Examples



D Reflection Across Y X Brainly Com



Reflection Mathbitsnotebook A1 Ccss Math



How To Find A Reflection Image



Reflection Objectives D Grade Reflect Shapes In Lines



Reflecting Shapes Article Reflections Khan Academy


Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download
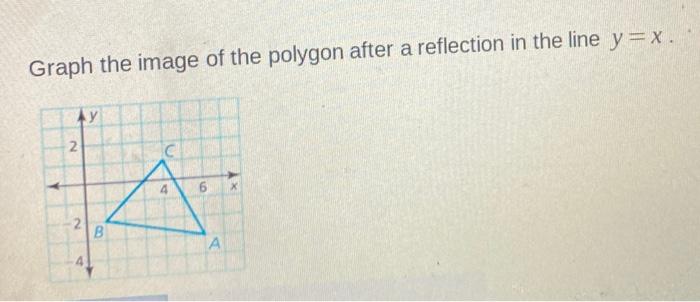


Solved Graph The Image Of The Polygon After A Reflection Chegg Com


How To Reflect A Graph Through The X Axis Y Axis Or Origin


What Does It Mean To Reflect Over The Y X Line Quora



Lesson On Line Of Reflection Y X



Is Reflected In The Line Y X Its Image Is B A
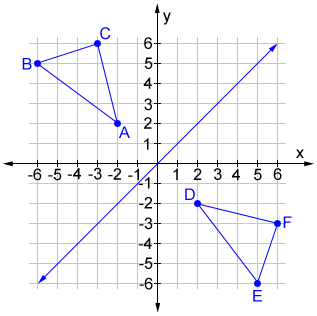


Reflection
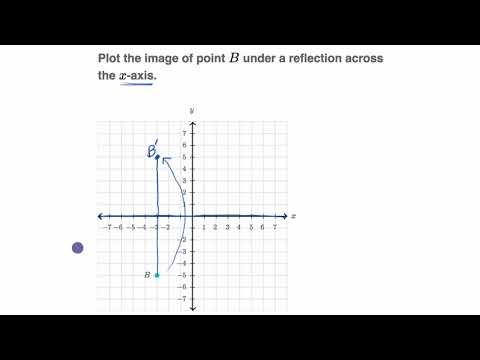


Reflecting Points Video Reflections Khan Academy



Reflection Over The Line Y X Math Showme



Reflection Over The Line Y X Geogebra



Transformations Boundless Algebra



Transformations Of Graphs
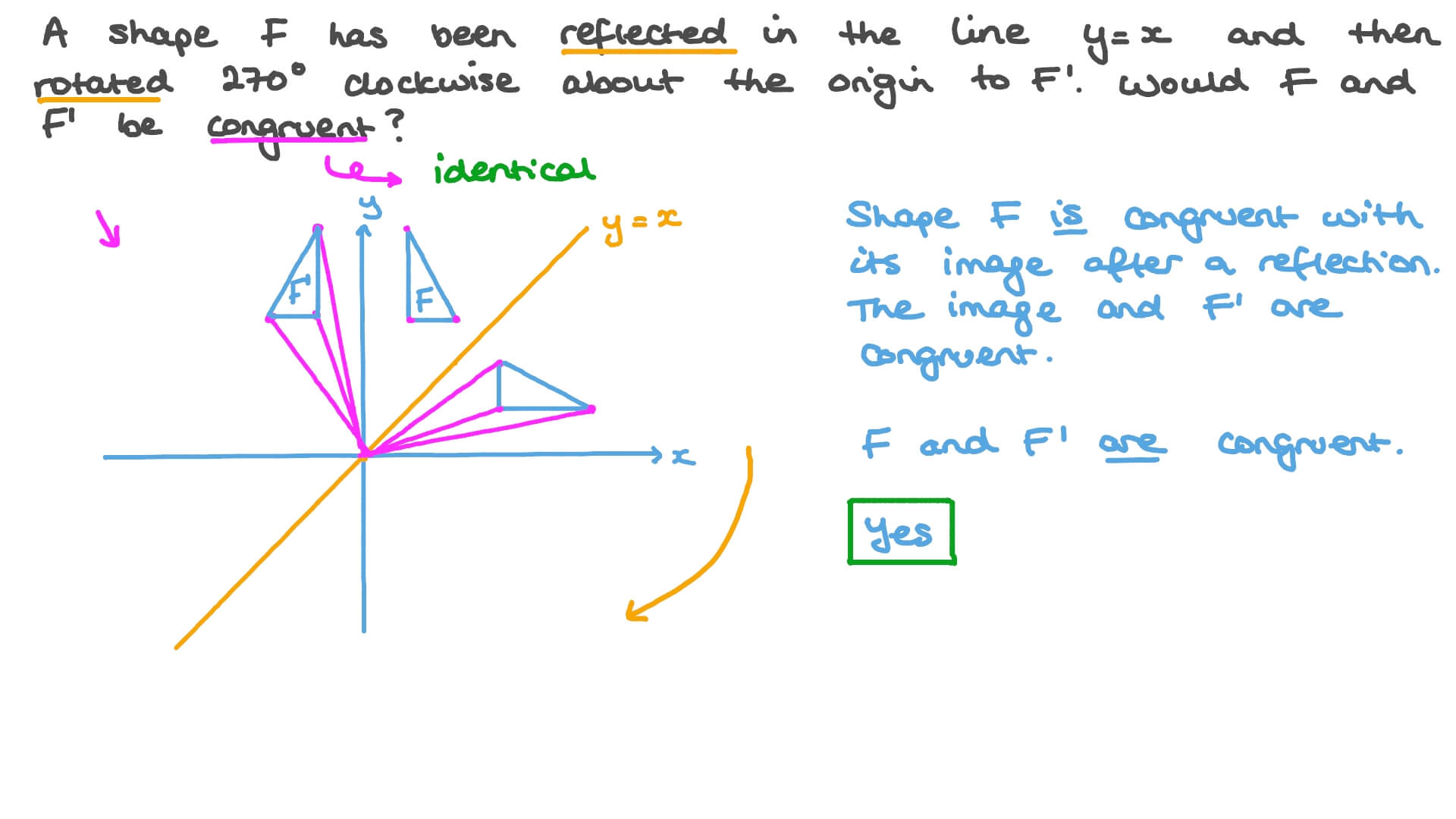


Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa
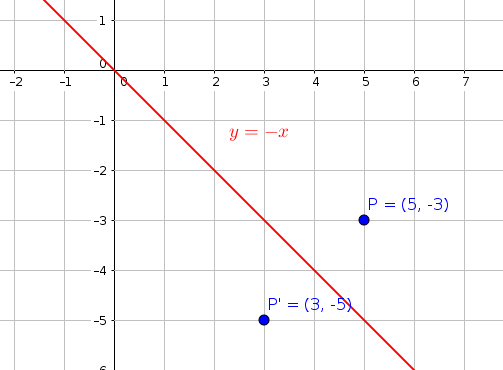


What Is The Reflection Image Of 5 3 In The Line Y X Socratic



Reflections Ck 12 Foundation



Geometry Transformations



Reflection Mathbitsnotebook A1 Ccss Math



Reflections Geometry Abroad


Math Alive Geometry 1



Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Reflection Rules How To W 25 Step By Step Examples



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines


Reflection Of A Point In A Line Assignment Point



Common Reflections Key Stage 3



What S The Image Of The Point 2 3 Reflected In The Line X Y 4 Quora



Transformation Reflection Over The Line Y X Youtube


Transformation Reflection Across Y X Youtube


Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines


Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa


9 3 Perform Reflections Reflection Transformation That Uses A Line Like A Mirror To Reflect An Image Line Of Reflection Mirror Line In A Reflection Ppt Download


Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q



Reflection Over The Line Y X Youtube



Reflection Mathbitsnotebook A1 Ccss Math



Describing A Reflection Key Stage 2
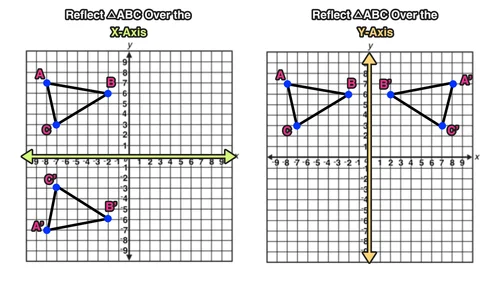


Reflection Over The X And Y Axis The Complete Guide Mashup Math



Why Do Points Get Exchanged When Reflected Across Line Y X Quora


Math Alive Geometry 1
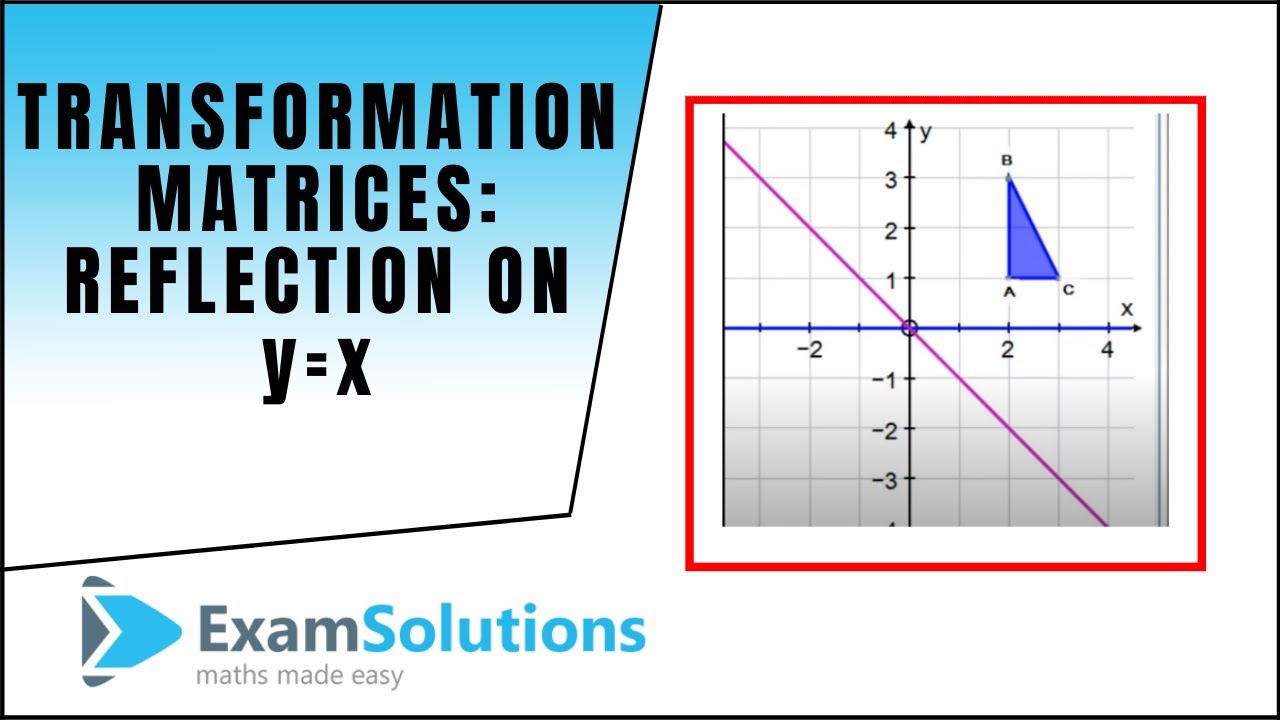


Reflections Reflection In The Line Y X Revisely



Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
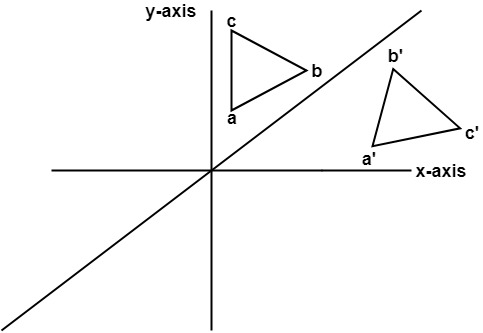


Computer Graphics Reflection Javatpoint
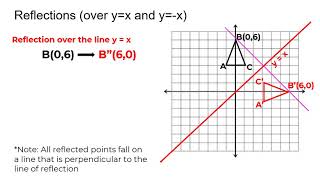


Reflection Over The Y X Line Youtube



How To Reflect A Line Segment Over The Y X Line Youtube


What Is The Image Of 2 5 Reflected Across X 2 Socratic



How To Find A Reflection Image



Reflections Across Y X Geogebra
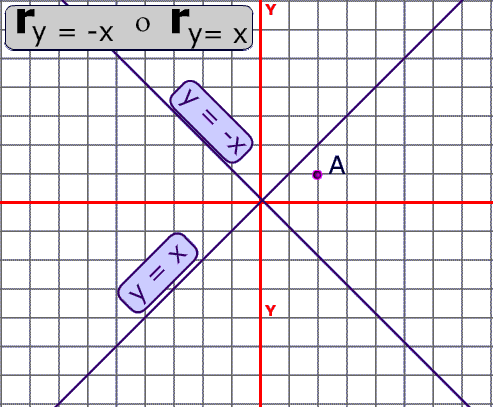


Compositions Of Reflections In Mathematics Theorems Involving Parallel And Intersecting Lines Interactive



Common Reflections Key Stage 3
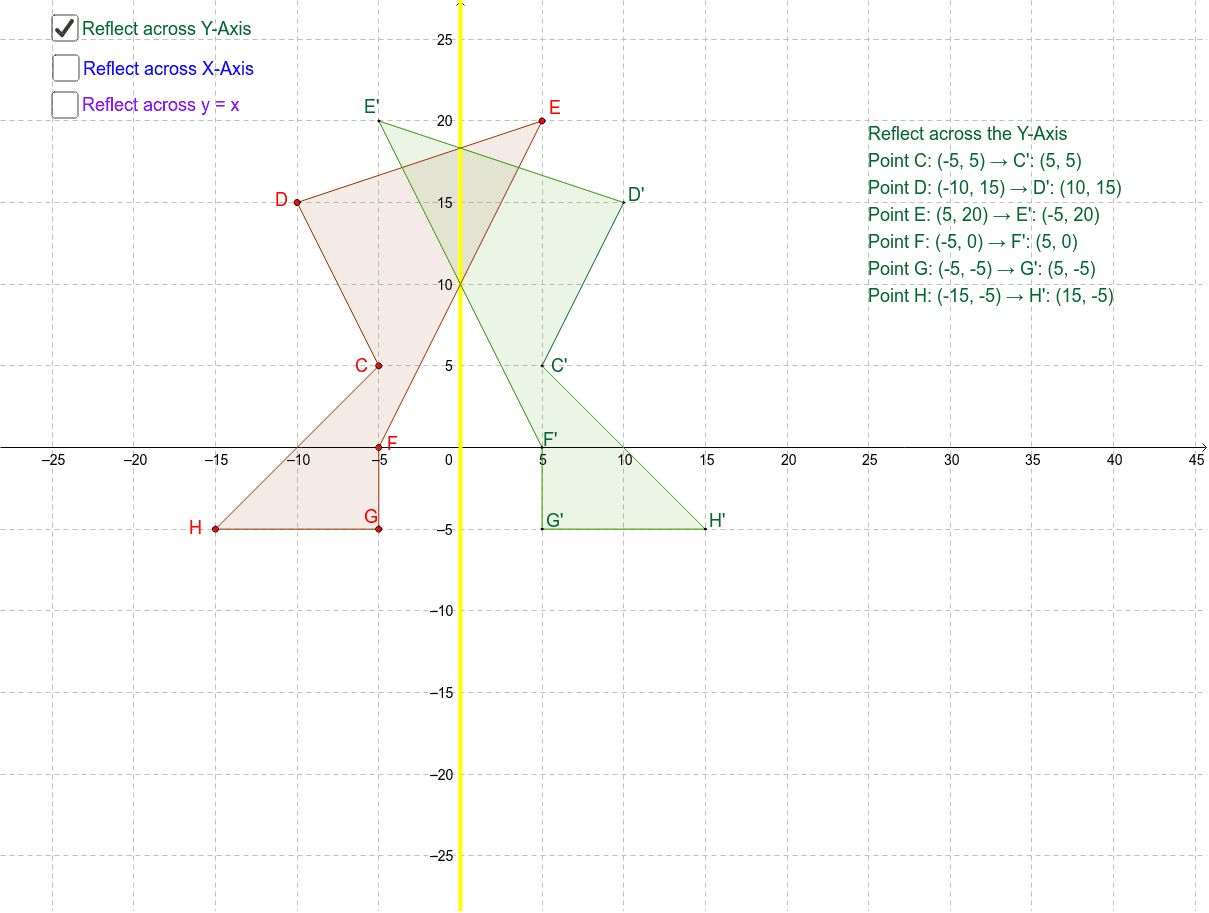


Reflections Across Axes And Y X Geogebra



Reflection In The Line Y X Geogebra



Picture Of Reflection Across Y Axis Reflection Math Reflection Math



Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math



Reflections Ck 12 Foundation


Geometric Reflections Q35 50 Intro To Geometry



Translation With Geogebra Figure 2 Reflection Through Line Y X With Download Scientific Diagram



Reflecting Shapes Video Reflections Khan Academy



0 件のコメント:
コメントを投稿