の体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方Feb 19, · このような球殻を \(t = 0\) から \(t = r\) まで足し合わせたものが半径 \(r\) の球であり、体積は \(\displaystyle \frac{4}{3} \pi r^3\) である。 よって、\(\Delta t\) を限りなく \(0\) に近づけると、球殻の体積について以下の式が成り立つ。球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集

中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
球 体積 求め方
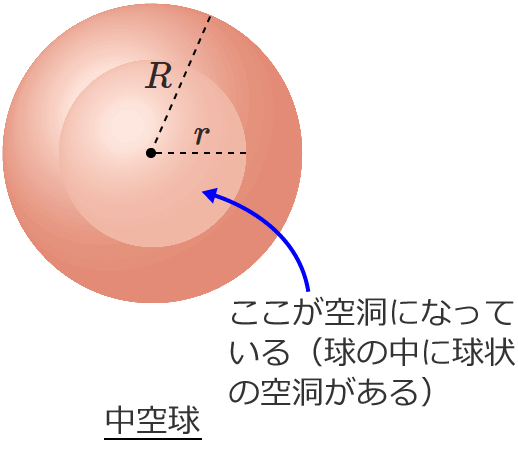
球 体積 求め方-Nov 09, 18 · 薄い球殻の体積を求めたい。 球殻は、中心を同じくする大きい球と小さい球とに挟まれた領域と言えるので、大きい球の半径を、小さい球の半径をとすると、体積は以下の式で表せる。 \begin{equation}V=\frac{4}{3}\pi (rdr)^3\frac{4}{3}\pi r^3\end{equation}体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
節洋傘を経由する球欠の体積 いた偏弧環を円錐台に加えた 「膨らんだ円錐台」 (右の上図) の体積を求めた。私は特に上が閉じた形を直観的に洋傘と呼ぶ。 これは関が9 と呼んだ立体に相当し、 これに中錐に相当する 体積を加えれば球欠の体積が得られる球の体積は、中心から表面までの距離 (常に一定)を半径rとすると、 4/3 * π * r3一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波センサー評価。 センサ直径、焦点深度が違うセンサを評価する際に、トータルの信号の何%を受けられているか計算
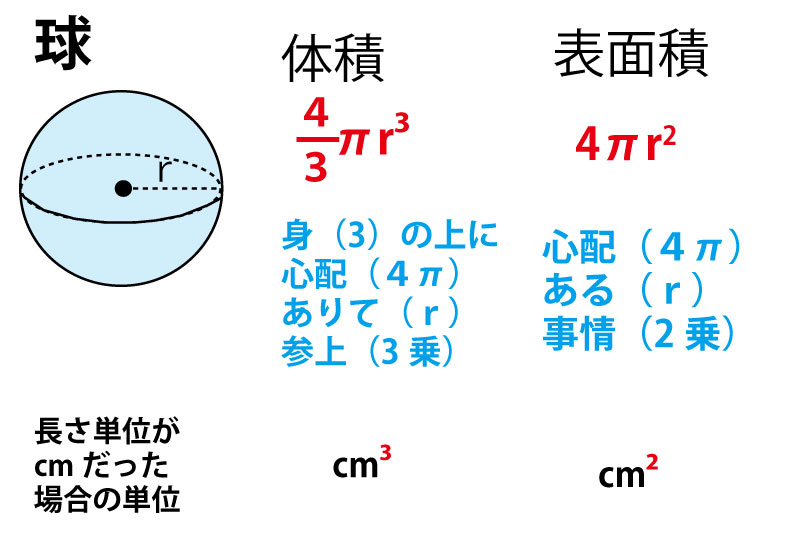
Jul 25, · 球の体積や表面積って、公式が複雑で覚えにくいですよね。そこでこの記事では、球の体積・表面積の公式の覚え方(語呂合わせ)や、公式の使い方をご紹介します!この記事を読めば、球の体積と表面積の公式を忘れることはもうありません!May 15, 15 · 球の表面積と体積のことかな!? 球の体積の求め方:「4/3πr³」 球の表面積の求め方:「4πr²」 だよ!May 12, 15 · 3分の4の理屈は中学校の場合 同じ直径2rと高さ2rを持つ円柱と比べると 体積比が球2対円柱3になるから円柱に対して球の体積は3分の2 円柱の体積=πr二乗×2r=2πr三乗 球=円柱の体積(2πr三乗)×3分の2 =3分の4πr三乗
Sep 21, · 下記の記事で、\(n\)次元空間の半径\(R\)の球の体積というのを求めました。 前回の記事はこちら n次元空間における半径Rの球の体積 ↑結果はこちらです。 せっかくなので、2次元、3次元、4次元、5次元の球の体積V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体Feb 28, 18 · 半球の体積を求める方法 元の球の状態の体積を求めて半分にしてやります。




球の体積 表面積 無料で使える中学学習プリント




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
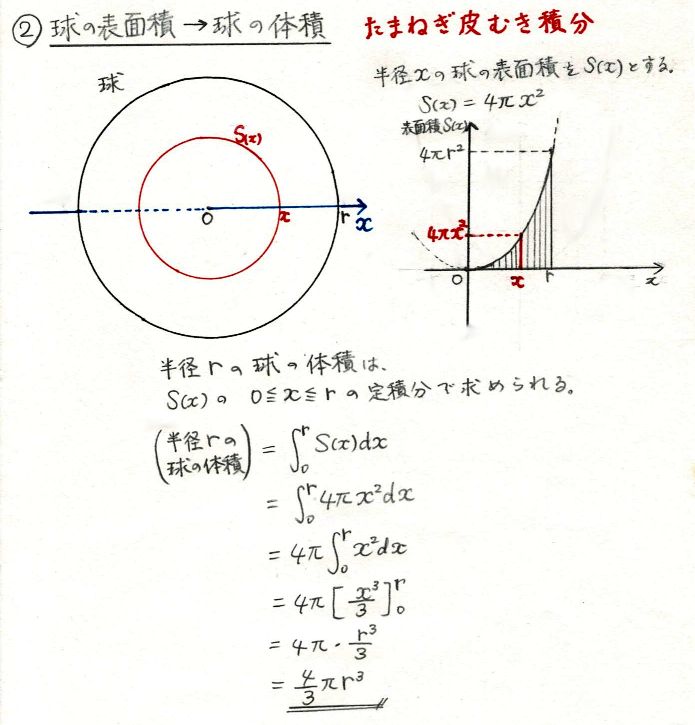
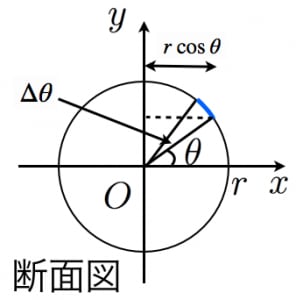
Jan 11, 19 · 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube



球の問題 苦手な数学を簡単に
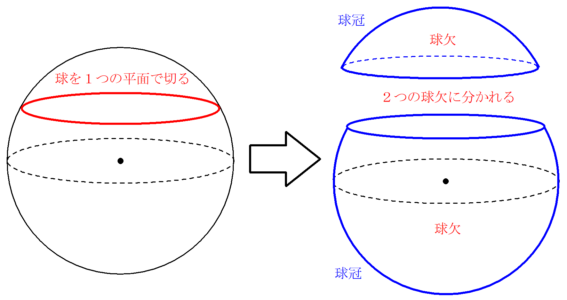
立体の表面積展開図(入試問題) → 携帯版は別頁 == 立体の体積(入試問題) == 要点四角柱,三角柱,円柱の体積 四角柱,三角柱,円柱の体積 V は,底面積 S と高さ h を使って表すことができます. V=Sh 特に,円柱については,底面の半径が rAug 28, · 球を1つの平面で切り取った部分である球欠について考えます。凸レンズの体積を求める際にも利用できます。 Ⅰ 球欠と球冠とは? Ⅱ 球欠の体積 Ⅲ 球冠の面積 Ⅰ 球欠と球冠とは? 言葉としAug 27, 18 · 回転体の体積の求め方 作成者 Bunryu Kamimura トピック 回転体の体積 回転体三角形 扇形の回転体 球欠+円錐の体積




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




球の体積と表面積 Jsciencer
球 帯と球冠 体積の大きさ(5:11)に引きずられて、計算で求めるまで同じになることが気付けませんでし 任意の位置でスライスした(正確な半球でないもの)場合の表面積の求め方人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。体積」 により、理解されることだろう。 球の表面積 S と体積 V の関係式で、「3分の1」が乗ぜられるのは、この「3分の1」であ る。 カヴァリエリの原理を用いて、球の体積は、次のようにして求められ



球の表面積の公式の求め方



うるおう微生物 口は災いのもと masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ
May 19, 17 · 球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して5004nnn π=125π (cm2) (答) ※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= 43n πr3 を半径で微分すると表面積 S=4πr2 になることが分かる.脱線ついでに言えば,円の面積 S=πr2 を半径で微分すると体積比 半径がrの球の体積をV、半径がkrの球の体積をV1とします。 よって、 が成り立ちます。 つまり、半径の比が1:kのとき、それらの球の体積比は となります。 ・ 角柱と角錐の性質と違い ・ 角錐と円錐の表面積の求め方 ・ 円柱と円錐の性質と違い




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear



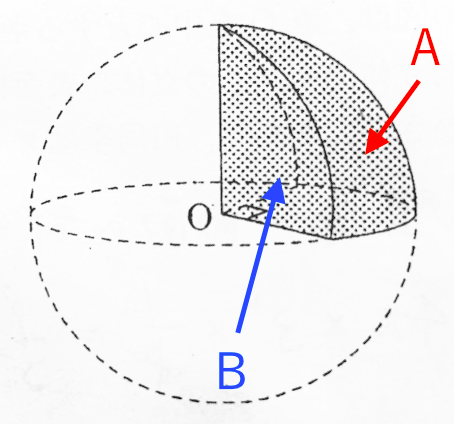
至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋
Feb , 19 · 球の体積の求め方の問題が解けていなかったので、驚きました。 確かに、球の体積の求めかたの公式、とっても覚えにくいですよね。 きょうは、その覚えにくい球の体積について、丸暗記ではない方法をお伝えします。 まず、こちらの図です。Mar 06, 21 · r r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。球欠,球台の体積 底面の半径が r 1 r_1 r 1 ,天面の半径が r 2 r_2 r 2 ,高さが h h h である球台の体積は, V = 1 6 π h ( 3 r 1 2 3 r 2 2 h 2 ) V=\dfrac{1}{6}\pi h(3r_1^23r_2^2h^2) V = 6 1 πh ( 3 r




ボード 数学 のピン




球の表面積と体積の求め方 苦手な数学を簡単に
今回は、体積の公式の求め方、覚え方と一覧、三角柱、円柱、三角錐の体積について説明します。 体積の意味など下記も参考になります。 体積の公式の覚え方は簡単です。球の体積を除けば、たった2つの公式を覚えるだけで済むからです。313 体積の計算 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 3 13 体積の計算 例 3 63 (球の体積) 半径 の球の体積は である. これを多重積分で求める.Nov 06, 18 · 球の体積、表面積の求め方例題 例題半径が2㎝の球について、体積と表面積を求めなさい。 半径が2㎝ということから、\(r=2\)となります。




中1 数学 6 5 球の体積 表面積 Youtube



1
Sep 06, 16 · 1:球の体積の求め方(公式) まずは球の体積の求め方(公式)を紹介します。 下の図のように、 半径rの球があるとき、球の体積は4πr 3 / 3 となります。Jan 14, · 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方Mar 31, 17 · πの求め方;




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活



Search Q E5 86 86 E6 9f B1 81 Ae E4 93 E7 8d Tbm Isch
球の体積の求め方でなぜ3分の4が出てくるのかわかりません。中1でもわかるように説明お願いします(>人<;) 縮め る球の表面積と体積 解く前に確認しよう ④ 球の表面積 半径が7の球の表面積をねとすると ぐー477" ④ 球の体積 半径1/2時 ・球の体積を求めることができる。 ・球の体積の求め方を理解する。 球の表面積の求め方を復習する。 本時の学習内容「球の体積の求め方を考えよう」を知る。 教科書180ページの「ひろげよう」に取り組む。 何杯分になるかを予想する。 全体




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




体積 10 球と円柱の共通部分 怜悧玲瓏 高校数学を天空から俯瞰する




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の体積と表面積を積分で証明 高校数学の美しい物語



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



2




球の表面積と体積の公式 数学fun




球の体積公式の微分が表面積になっている理由 Youtube




球の体積の求め方を教えていただけませんか よろしくお願いしますm M Clear




球の表面積の求め方 公式と計算例




球の体積と表面積 Youtube



球欠と球冠 Fukusukeの数学めも




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中1数学 球 練習編 映像授業のtry It トライイット



球の体積 簡単に計算できる電卓サイト
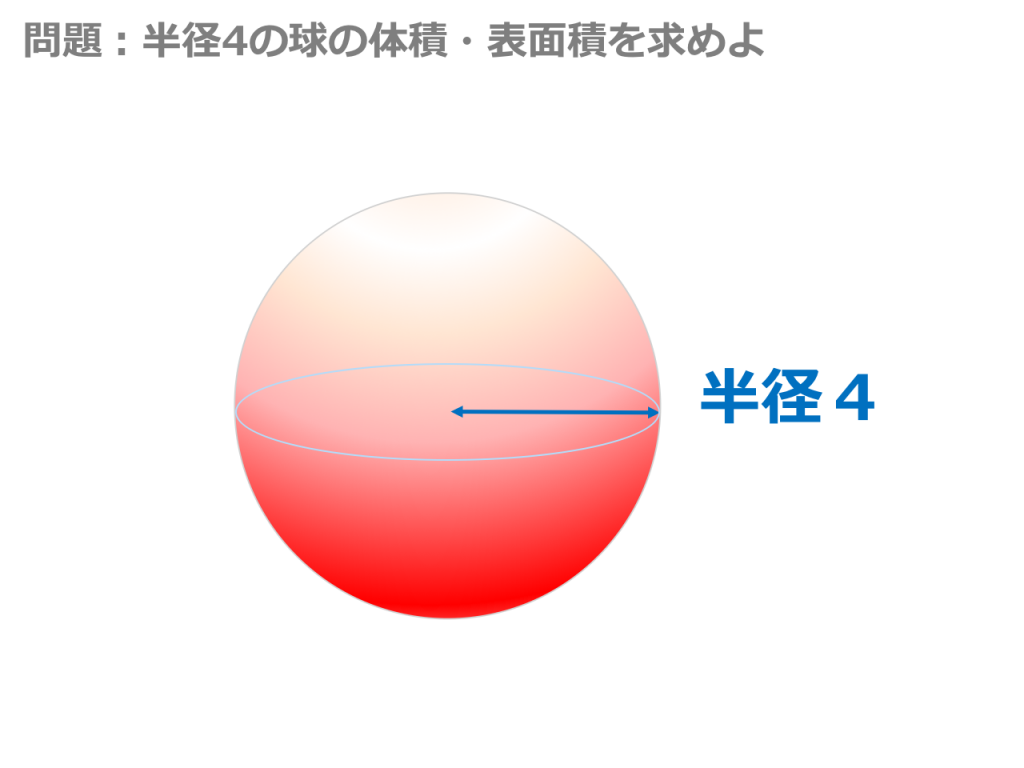



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
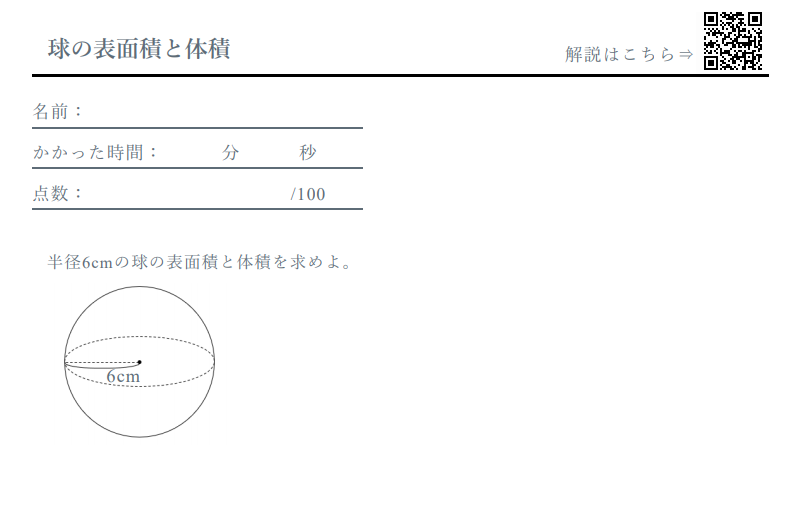



球の表面積と体積 計算ドリル 問題集 数学fun




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球の表面積と体積の公式 数学fun



Q Tbn And9gcqqgrizekrnz Lytyjejolqml9yfhpazps6kyq0k Jpevu2dxgk Usqp Cau




球の表面積と体積の公式 数学fun




半球の体積と表面積を計算する 具体例で学ぶ数学




球の表面積と体積の公式 数学fun




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球の表面積 体積 身勝手な主張




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



中1数学 球の表面積と体積の求め方と練習問題 Atstudier




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要




球の表面積と体積の公式 数学fun




角錐 円錐の体積と表面積の公式 数学fun




球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト
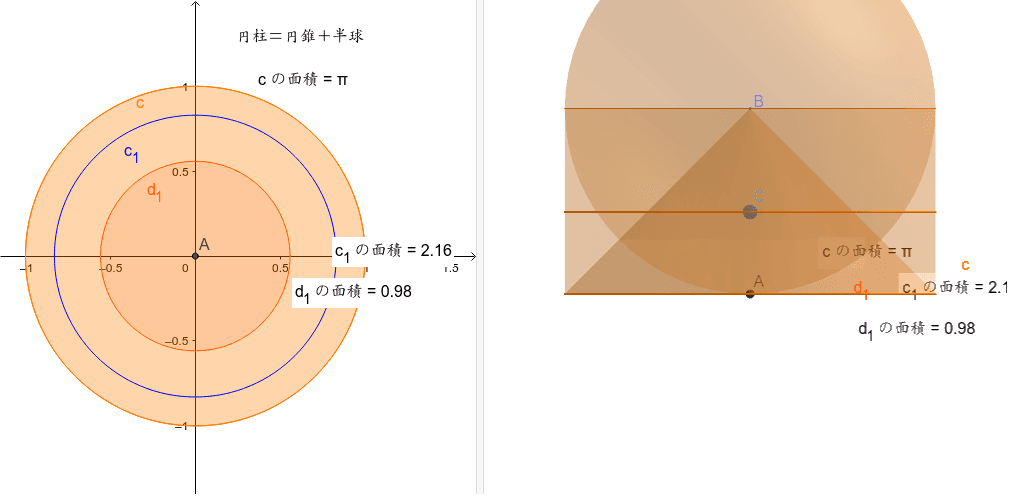



球の体積の求め方 Geogebra




これまでで最高の面積 球 の 体積 の 求め 方 最高のぬりえ



Q Tbn And9gcqwkabdudclaf 47vgw O93wu16c0ercc O5o6eo6xp177ses0w Usqp Cau



研究




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



立体 の 表面積 求め 方



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の表面積の求め方 その3 感じる科学 味わう数学




中学数学 空間図形 体積の問題のコツ
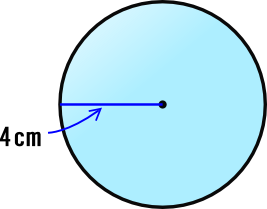



中学1年数学練習問題 球の体積と表面積の求め方と解答 空間図形




球の体積と表面積 公式と計算問題と証明 Irohabook




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ




初等幾何 球の表面積を求める 大人が学び直す数学
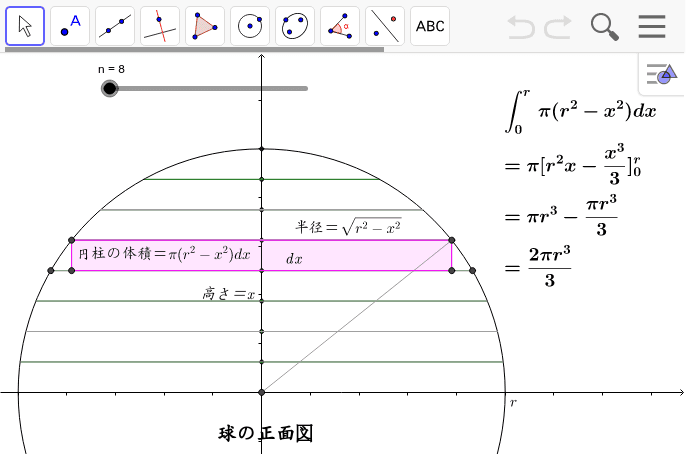



球の体積の積分 Geogebra



Studydoctor球の表面積や体積の公式と求め方 中学1年数学 Studydoctor



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




この答えは2p になるんですが この球の体積の求め方とどうやったらこの答えに Clear




中1数学 球 例題編 映像授業のtry It トライイット




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Yogb6 Tjpto Wm




球の表面積の公式について みたにっき はてな




中1数学 空間図形 球の体積の求め方 Youtube



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
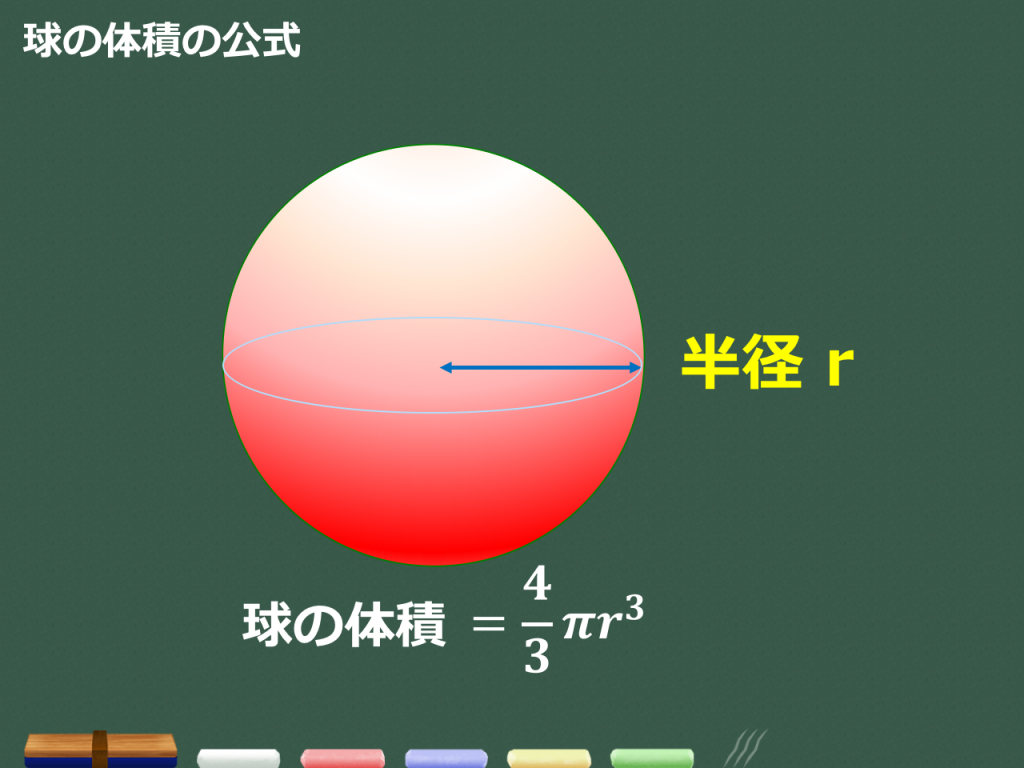



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




球に関する公式 理数系無料オンライン学習 Kori




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



大学入試問題




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の体積と表面積を積分で証明 高校数学の美しい物語




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



球の体積 高精度計算サイト




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積 球の表面積の公式の導出 積分 優技録




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の体積の求め方 感じる科学 味わう数学




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




中1 数学 中1 84 球について Youtube




球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の体積を重積分で求めたいのですが 上手くいきません は球の上半分 半球 Yahoo 知恵袋



立体の体積を求める公式
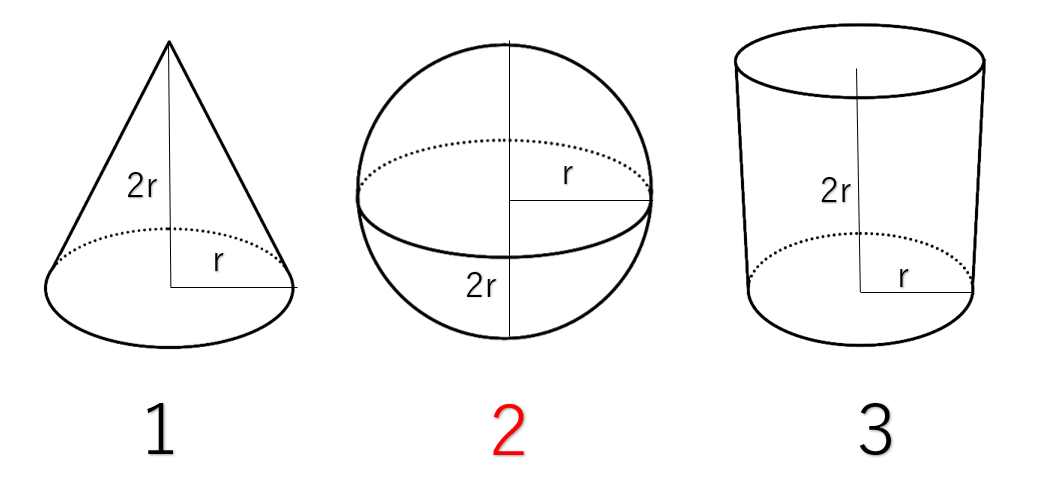



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾



0 件のコメント:
コメントを投稿