Q261 1 Verify that μ ( x, y) = y is an integrating factor for (A) y d x ( 2 x 1 y) d y = 0 on any open rectangle that does not intersect the x axis or, equivalently, that (B) y 2 d x ( 2 x y 1) d y = 0 is exact on any such rectangle Verify that ySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more X y 2 dx 2xy x 21 dy 0 y 1 1Help is appreciated EditFind the particular solution of the differential equation (1 – y^2) (1 log x) dx 2xy dy = 0, given that y = 0 when x = 1 CBSE CBSE (Commerce) Class 12 Question Papers 1786 Textbook Solutions Important Solutions 3417 Question Bank Solutions 153 Concept Notes & Videos 447

For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube
(x^2+y^2)dx-2xy dy=0 integrating factor
(x^2+y^2)dx-2xy dy=0 integrating factor-The solution of the differential equation (x^2 y^2) dx 2xy dy = 0 isSimple and best practice solution for (x^2y^2)dx(x^22xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for (x^2y^2)dx(x^22xy)dy=0
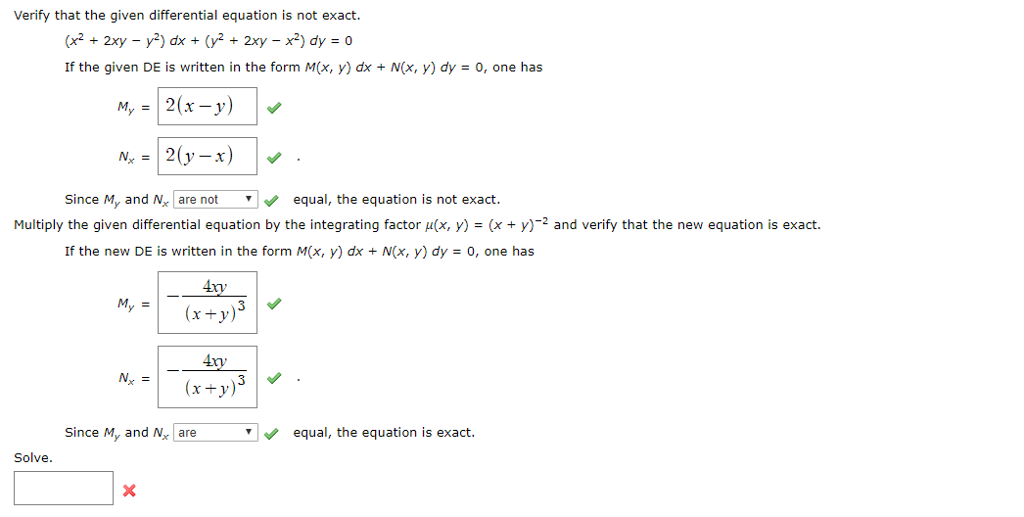



Verify That The Given Differential Equation Is Not Chegg Com
I got mu(y) = e^y The point of an integrating factor is to turn an inexact differential into an exact one One physical application of this is to turn a path function into a state function in chemistry (such as dividing by T to turn q_"rev", a path function, into S, a state function, entropy) I assume that the second terms include 3y^2, not 3y (it would be odd to not simply write 9y)INTEGRATING FACTOR BY FORMULA a)2y(x 2 y x) dx 2 (x 2 2y) dy = 0 b)(7xy y 2) dx 8y 2 dy = 0 c)x 2 y 3 dx x(x 2 y 2 xy 7) dy = 0 d)(3x 2 y 2) dx 2xy dy = 0 Expert Answer Who are the experts? (𝑥^2−𝑦^2 )𝑑𝑥2𝑥𝑦 𝑑𝑦=0 Step 1 Find 𝑑𝑦/𝑑𝑥 (𝑥^2−𝑦^2 )𝑑𝑥2𝑥𝑦 𝑑𝑦=0 2xy dy = − (𝑥^2−𝑦^2 ) dx 2xy dy = (𝑦^2−𝑥^2 ) dx 𝑑𝑦/𝑑𝑥 = (𝑦^2 − 𝑥^2)/2𝑥𝑦 Step 2 Putting F(x, y) = 𝑑𝑦/𝑑𝑥 and finding F(𝜆x, 𝜆y)
They give you the integrating factor is x 2 , so multiply the whole equation by said factor to get (1y 2 /x 2 )dx (12y/x )dy = 0 Now, check for exactness again, dM/dy = dN/dx (these should be partial derivatives) dM/dy = 2y/x 2 dN/dx = 2y/x 2 Therefore this equation is now exact, and solve it like you would any other exact equationX ( x 2 − 3 y 2 x y) = 0 d x ( x 2 3 y 2 x y) = 0 d x(x2 − 3y2 xy) = 0 d x ( x 2 3 y 2 x y) = 0 d If any individual factor on the left side of the equation is equal to 0 0, the entire expression will be equal to 0 0 x = 0 x = 0 x2 − 3y2 xy = 0 x 2 3 y 2 x y = 0 Set the first factor equal to 0 0 最も好ましい (x y)^2 dx (2xy x^21)dy=0 (xxy^2)dx(1x^2)dy=0 リンクを取得 ;
Click here👆to get an answer to your question ️ An integrating factor for the DE (1 y^2)dx (tan^1y x)dy = 0 isIn Maths, an integrating factor is a function used to solve differential equations It is a function in which an ordinary differential equation can be multiplied to make the function integrable It is usually applied to solve ordinary differential equations Also, we can use this factor within multivariable calculus When multiplied by an integrating factor, an inaccurate differential is made (x^(2)y^(2)) dx 2xy dy = 0 Updated On 1 To keep watching this video solution for FREE, Download our App The integrating factor of the differential equation is Class 12th DIFFERENTIAL EQUATIONS Verify that




9 A Show That X X2 Y2 1 Is An Integrating Fac Math




Lesson 6 Exact Equations Determine Whether Or Not Each Of
Show that {*(x² y²))1 is an integrating factor of the equation (x² y²) dx 2xy dy = 0 and hence solve the equation Answer Find an integrating factor and solve the following equations (3x2y 2xy y3)dx (x2 y2)dy = 0 Show transcribed image text Solve (x y)dx (x – y) dy = 0 Solve (x – y^2) dx 2xy dy = 0 Solve dy/dx = 4 y^2/1 x^2 Solve (ye^xy – 1/y) dx (xe^xy x/y^2) dy = 0 Solve dy/dx y/x = x^2y^2, x > 0 Solve (x 3x^3sin y) dx x^4 cosy dy = 0 given that the function mu(x, y) = x^1 is an integrating factor Solve 1/x dy/dx – 2y/x^2 = x cosx, x > 0 Solve dy/dx = 1 x^2 y




Pdf Lesson 4 Homogeneous Differential Equations Of The First Order Luis Adolfo Ibarra Sansuste Academia Edu




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more (X^2Y^2)DxXydy=0 The term within parentheses is recognizable as the exact differential d(y^2/x) ( ^2 ^2 ^2)/(2 ^2 ) The order and degree of the differential equation are √(d^2y/dx^2) = √(dy/dx 5) respectively Differentiating wrtx / = x / ( ^2 ^2 ^2)/(2 ^2 ) v x / = ( ^2 ^2 ^2 2 ^2 ^2 This make think that probably there are some mistakes in your analytical calculus
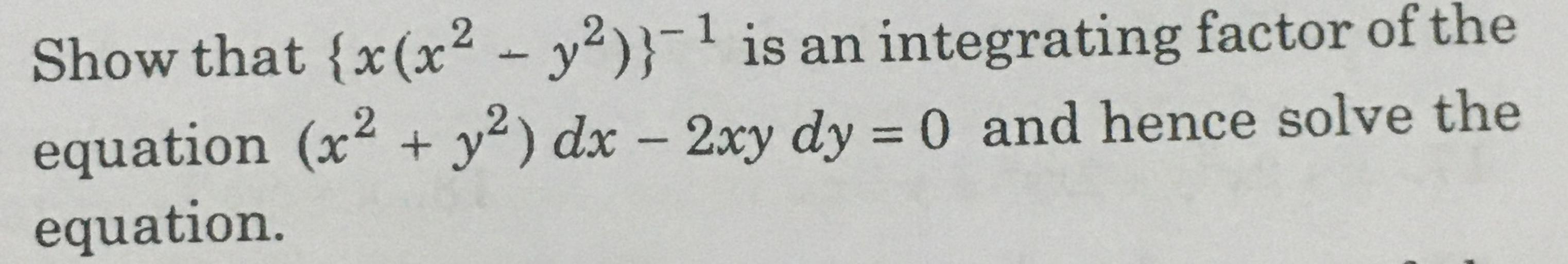



Show That X Y 1 Is An Integrating Factor Of Th Math




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5
Ex 9 5, 4 Show homogeneous (x2 y2) dx 2xy dy = 0 Solved Dy/dx = X2 2y/x (2x Y)dy = (2y X)dx (1 Exy How do you solve dy/dx = y^2xsqrt(1 x^2) where y=1 when Advertisiment Ex 9 5, 9 Show homogeneous y dx x log (y/x) dy 2x Ex 9 6, 9Transcribed Image Textfrom this Question Consider the equation (y^2 2xy)dx x^2 dy = 0 Show the equation is not exact, but becomes exact if we multiply it by y^2 Use the resulting exact equation to find the general (implicit) solution of the original equationY = 10x, where P(x) = 2 x, Q(x) = 10x Integrating factor IF = e R P(x)dx = e2 R dx x = e2ln x = eln x 2 = x2 Multiply equation x2 dy dx 2xy = 10x3 ie d dx x2 ·y = 10x3 Integrate x2y = 5 2 x4 C ie y = 5 2 x2 C x2 Toc JJ II J I Back Solutions to exercises 18 Particular solution y(1) = 3 ie y(x) = 3 when x = 1 ie 3 = 5 2 ·1 C 1 ie 6 2 = 5 2 C ie C = 1 2 ∴ y = 5 2 x 2




Dy Dx X2 Y2 2xy Novocom Top



3
$M~dx N~dy = 0$ $(x^2 y^2 1)~dx x(x 2y)~dy = 0$ $M = x^2 y^2 1$ $N = x(x 2y) = x^2 2xy$ $\dfrac{\partial M}{\partial y} = 2y$(c) ( y 2 x y 1 ) dx ( x 2 x y 1 ) dy = 0With M = y 2 x y 1 and N = x 2 x y 1, note that ( N x M y) / ( x M y N ) = ( x y ) / ( x ( y 2 x y 1 ) y ( x 2 x y 1 ) ) = ( x y ) / ( x y) = 1 Thus, μ = exp ( ∫ d(xy) ) = e xy is an integrating factor The transformed equation is ( y 2 x y 1 ) e xy dx ( x 2 x y 1 ) e xy dy = 0 For the differential equation `(x^2y^2)dx2xy dy=0`, which of the following are true (A) solution is `x^2y^2=cx` (B) `x^2y^2=cx` `x^2y^2=xc` (D) `y (A) solution is `x^2y^2=cx` (B) `x




X2 Y2 Dx 2xydy 0 Brainly In




Solve The Following Differential Equations 1 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Youtube
In order to find the Integrating factor, solve the value of =1/x Since the value obtained is purely a function of x, we can conclude that the special integrating factor is = e lnx = x Multiply the special integrating factor with the original equation, x(2y 2 2y4x 2)dx (2xy x) dy=0 (2xy 2 2xy4x 3)dx (2x 2 y x 2) dy=0Dividing the entire equation by ' dx ' gives us(1yx2y) dxdy (xx3) =0dxdy xx3y(1x2) = xx3−1 dxdy x(1x2)y(1x2) = xx3−1 dxdy xy = xx3−1 dxdy yP (x) = Q(x)Hence, I F = e∫ P (x)dx= e∫ x1 dx= elog(x)= x Answer verified by Toppr 67 Views The given differential equation is not exact and I think you can't find the integrating factor by known way and an easier way, rather you can solve it as follows (x2 − y2 − y)dx − (x2 − y2 − x)dy = 0 (x2 − y2)(dx − dy) xdy − ydx = 0 (1 − y2 x2)(dx − dy) xdy − ydx x2 = 0 (1 − y2 x2)(dx − dy) d(y x) = 0



Search Q X 5e2 3y 5e2 Dx 2xy Dy 3d0 Tbm Isch




Solve The Differential Equation Dy Dx 2xy 1 X 2 X 2 2 Maths Differential Equations Meritnation Com
(x y)^2 dx (2xy x^21)dy=0 (1x^2y^2x^2y^2)^1/2xy dy/dx=0 Feb 14, 17 Here is the equation $$(2xyx^2x^4)\,dx(1x^2)\,dy=0$$ It is not exact since partial derivatives are not equal Any help would be appreciated ordinarydifferentialequations Share Cite $$\frac {1}{1x^2}y = \int \frac {x^2}{1x^2}\\ \frac {1}{1x^2}y = x \arctan x C\\ y = x^3 x (1x^2)\arctan x C(1x^2)$$ Share Cite (3y^22xy)dx (2xyx^2)dy=0 classify the equation linear, nonlinear, separable,exact, homogeneous, or one that requires an integration factor Download PDF PrintThat is a function of only one variable, and solve the given equation 3 ydx − xdy = 0 4 3x2ydx 2x3dy = 0 5 2y3dx 3y2dy = 0 6 (5xy 2y 5)dx 2xdy = 0 7 (xy x 2y 1)dx (x 1)dy = 0 8 (27xy2 8y3)dx (18x2y 12xy2)dy = 0




Write The Integrating Factor Of 1 Y2 2xy Coty Dy Dx Scholr




Pdf 2 6 Exact Differential Equations And Integrating Factors Mirna Mansour Academia Edu
113k views asked in Class XII Maths by nikita74 (1,017 points) Find the general solution of y 2 dx (x 2 xyy 2 )dy = 0 differential equations For the differential equation `(x^2y^2)dx2xy dy=0`, which of the following are true (A) solution is `x^2y^2=cx` (B) `x^2y^2=cx` `x^2y^2=xc` (D) `yWe have, \ \left( x^2 3xy y^2 \right) dx x^2 dy = 0\ \ \Rightarrow \frac{dy}{dx} = \frac{x^2 3xy y^2}{x^2}\ This is a Q262 In Exercises find an integrating factor;




Verify That The Given Differential Equation Is Not Chegg Com




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top
Re write as dx (dx y^2–2ydy)/x^2=0 d(x) d(y^2/x)=0 integrating u get x y^2/x=c is the solution where c is an arbitrary constant is the solutionตัวประกอบเพื่อการอินทิเกรต 2Integrating Factor 2 (y^2)dx((x^2)xy)dy=0http//wwwmathunivercom/p/blogpageClick here👆to get an answer to your question ️ Solve the differential equation (x^2 y^2) dx 2xydy = 0



1



Exact Equations
asked in Mathematics by Ankitk (741k points) If integrating factor of x (1 – x2)dy (2x2y – y – ax3) dx = 0 is e∫p∙dx, then p is equal to (A) 2x2 – 1 (B) {2x2 – 1}/ {x (1 – x2)} {2x2 – ax3}/ {x (1 – x2) (D) ax3 differential equations jee jee mainsDy Dx 2xy F X Y 0 2, Ex 9 6, 14 Find particular solution (1 x2) dy/dx 2xy, Solve the differential equation dy/dx = (2y x) / (2x y, Ex 9 5, 12 Find particular solution x2 dy (xy y2, *Differential Equation dy/dx=x(y 1)^2 with initialSimple and best practice solution for (x^2y^2)dx(x^22xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for (x^2y^2)dx(x^22xy)dy=0



Http 1 160 97 198 8080 Xmlui Bitstream Handle 2 2 chapter 1 11 Pdf Sequence 2




Dy Dx 2xy Novocom Top
A Suppose we have M(x,y) dx = N(x,y) dy Then the DE is exact if M_yN_x=0 M = 6xy 3y^22y => M_y = 6x6y2 N= 2(xy) => N_x = 2 M_y N_x != 0 => Not an exact DE So, we seek an Integrating Factor mu(u) such that (muM)_y = (muN)_x So, we compute (M_yN_x)/N = (6x6y2 2)/(2(xy)) = 3 So the Integrating Factor is given by mu(x) = e^(int \ 3 \ dx) \ \ \ \ \ \ \5月 05, 21 Simple and best practice solution for (2xy)dy(x^2y^21)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your(2y2 3x) dx 2xy dy = 0 Sometimes we can find an integrating factor µ(x,y) so that the equation obtained by multiplying by µ(x,y) (shown below) is exact µ(x,y)M(x,y) dx µ(x,y)N(x,y) dy = 0 Exact Differential Equations Solving an Exact DE Making a DE Exact Conclusion Using an Integrating Factor In order for our integrating factor to work, we need the following to be exact µ(x,y)M(x
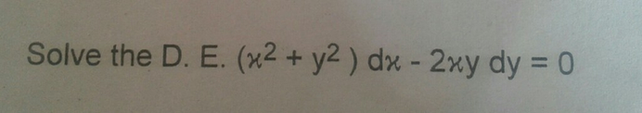



Solve The D E X2 Y2 Dx 2xy Dy 0 Scholr
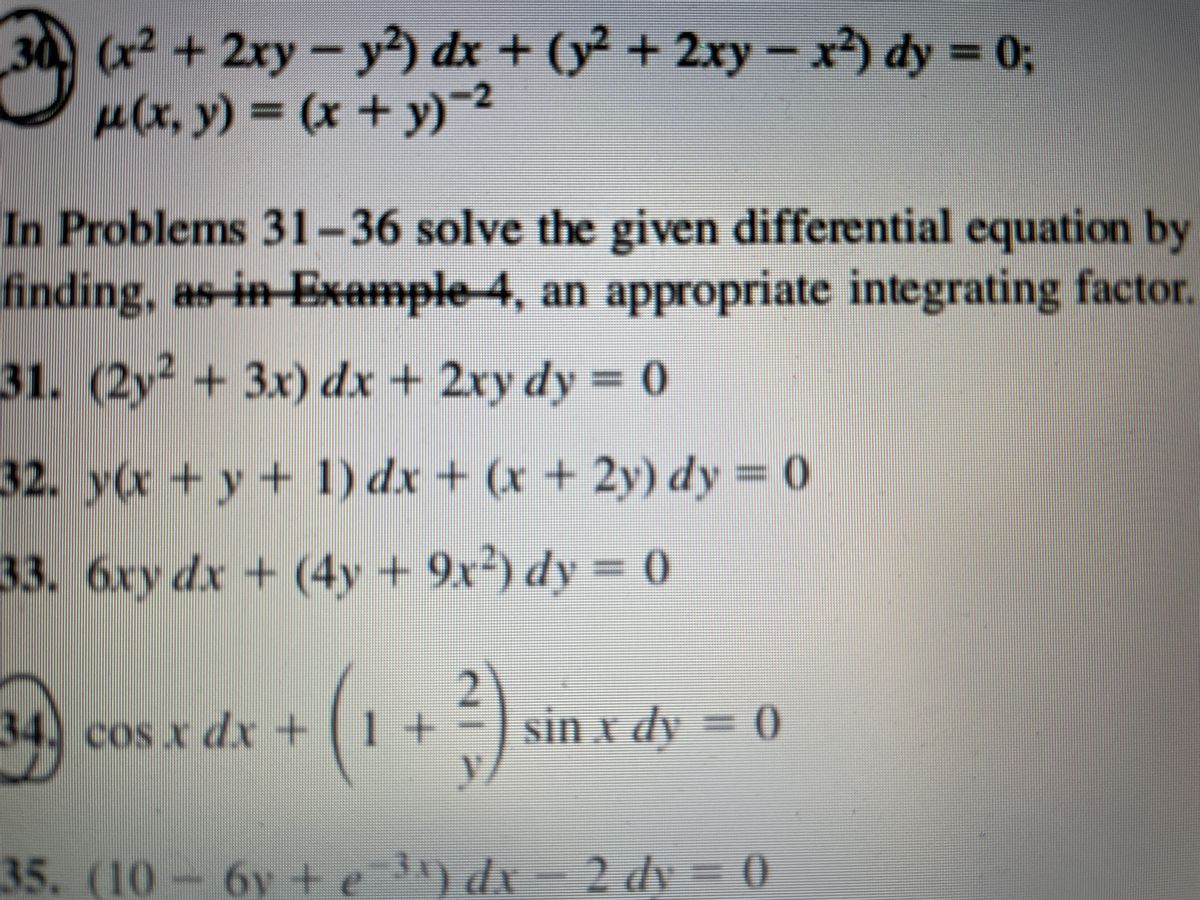



Answered In Problems 31 36 Solve The Given Bartleby
Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Previous question Next questionFind the corresponding particular solution for {eq}\displaystyle (x^2y^2)\ dx 2xy\ dy=0 {/eq} using the integrating factor Using an Integrating Factor The given equation is in the form of (x^22xyy^2)dx(x y)^2 dy= Find the particular solution of the differential equation (3xy y^2)dx (x^2 xy)dy = 0, for x = 1, y = 1 asked Nov 17, 18 in Mathematics by monuk ( x^2y2y^23x64=0 Given DE (2xy3)dx(x^24y)dy=0 Comparing above equation with the standard form of DE MdxNdy=0 we get M=2xy3\implies \frac{\partial M}{\partial y}=2x & N=x^24y\implies




Solve The Differential Equation X 2 Y 2 Dx 2xydy 0




Aem Integrating Factor To Orthogonal Trajactories
Get an answer for 'solve the differential equation (2xy3y^2)dx(2xyx^2)dy=0 ' and find homework help for other Math questions at eNotesX 2 Y 2 Dx 2xy Dy 0 Youtube (x^22xyy^2)dx(x y)^2 dy=0 (x^22xyy^2)dx(x y)^2 dy=0Simple and best practice solution for (x^2y^2)dx(x^22xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your ownDifferential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



Projecteuclid Org Ebook Download Urlid 10 3792 2fchmm 2f Isfullbook False




Doc Differential Equations Tt Arafat Rahman Academia Edu




Exact Differential Equations



Solved Test Exactness And Solve Question 1 2xy 3x 2 Dx X 2 2y Dy 0 Question 2 Cosx Xsinx Y 2 Dx 2xydy 0 Question 3 2xydx X 2 Course Hero




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube



Y 4 2xy Dx 3x 2 Dy 0 Brainly Ph




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download




X 2 Y 2 Dx 2xy Dy 0 Youtube
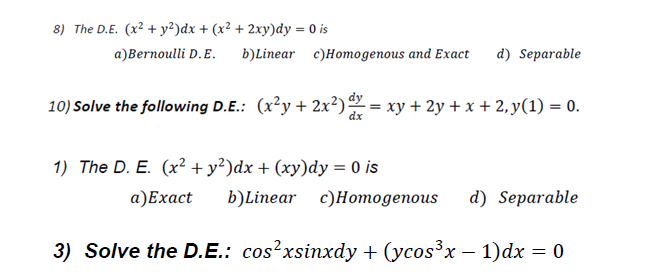



The D E X 2 Y 2 Dx X 2 2xy Dy 0 Is Chegg Com




9 A Show That X X2 Y2 1 Is An Integrating Fac Math




Solved Problems In Differential Equations 2500 Solved Problems In Differential Docsity




Math 432 Hw 2 5 Solutions Pdf Free Download




Math 432 Hw 2 5 Solutions Frostburg




How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora




Number 5 Please 1 14 Odes Integrating Factors Test For Exactness If Exact Solve If Not Use Homeworklib




Math 432 Hw 2 5 Solutions Pdf Free Download



How To Solve The Differential Equation X Y Dx 2xydy 0 Quora



The Solution Of 1 X 2 Dy Dx 2xy 4x 2 0 Is Sarthaks Econnect Largest Online Education Community



Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline




In Solve The Given Initial Value Problem X Y 2 Chegg Com




Consider The Differential Equation 2y 2 3x Dx Chegg Com




Suggested Problems Engr213 Concordia Studocu




Solve 3xy 2ay 2 Dx X 2 2axy Dy 0 Mathematics Stack Exchange




Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation




Math 432 Hw 2 5 Solutions Pdf Free Download




How Does One Solve 2xy Dx X 2 1 Dy 0 With The Homogeneus Method Quora




15 The Differential Equation 2xy Dy X2 Y2 1 Dx Determines A A Family Of Circles With Centre On X Axis B A Family Of Circles With Centre On Y Axis




Question 1 Let Y Be A Function Of X Identify Do Not Solve The Following Equations Homeworklib




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Solve The Following Ordinary Differential Equation 2y 2 2y 4x 2 Dx 2xy X Dy 0 Wegglab




What Is The Solution To This Ode 3x 2 4xy Y 2 Dx 2x 2 2xy 9 Dy 0 Quora




Exact Non Differential Equation




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




He A 1 8 B 11 8 C 3 8 The Differential Equation Of The System Of Circles Touching The X Axis At Origin A X2 Y2 Dy Dx 2xy 0 B X2 Y Dy Dx 2xy 0 C X Y




Solve The Differential Equation X 2y Dx 2x Y Dy 0 Youtube




Nonexact De Made Exact 2y 2 9x Dx 2xydy 0 Youtube



Solved Find An Integrating Factor And Solve The Equation Ydx 2xy E 2y Dy 0 Y 0 Course Hero




X 2 Y 2 Dx 2xy Dy 0 Novocom Top



Solve The Differential Equations 1 X 2 Dy Dx 2xy X 1 X 2 Sarthaks Econnect Largest Online Education Community




Integrating Factors 1 Video Khan Academy



Find An Integrating Factor And Solve The Following Equations 3x 2y 2xy Y 3 Dx X 2 Y 2 Dy 0 Sarthaks Econnect Largest Online Education Community



2




Math 432 Hw 2 5 Solutions Pdf Free Download



How To Solve X Y Dx 2xy Dy 0 Quora




X2 1 Dy Dx 2xy X4 2x2 1 Cos X Solve This Differential Maths Differential Equations Meritnation Com



Solve The Differential Equation Dy Dx 2xy Y Studyrankersonline




Solved The Equation 2y2 2y 4x2 Dx 2xy X Dy 0 Chegg Com




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




Exact Non Differential Equation




9 Solve Dy Dx 2xy X 2 Y 2 10 Solve 2xydx 1 Chegg Com




Number 5 Please 1 14 Odes Integrating Factors Test For Exactness If Exact Solve If Not Use Homeworklib




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




Hw 2 5 Solutions Pdf




Exercises 2 4 Answers To Selected Odd Numbered Chegg Com
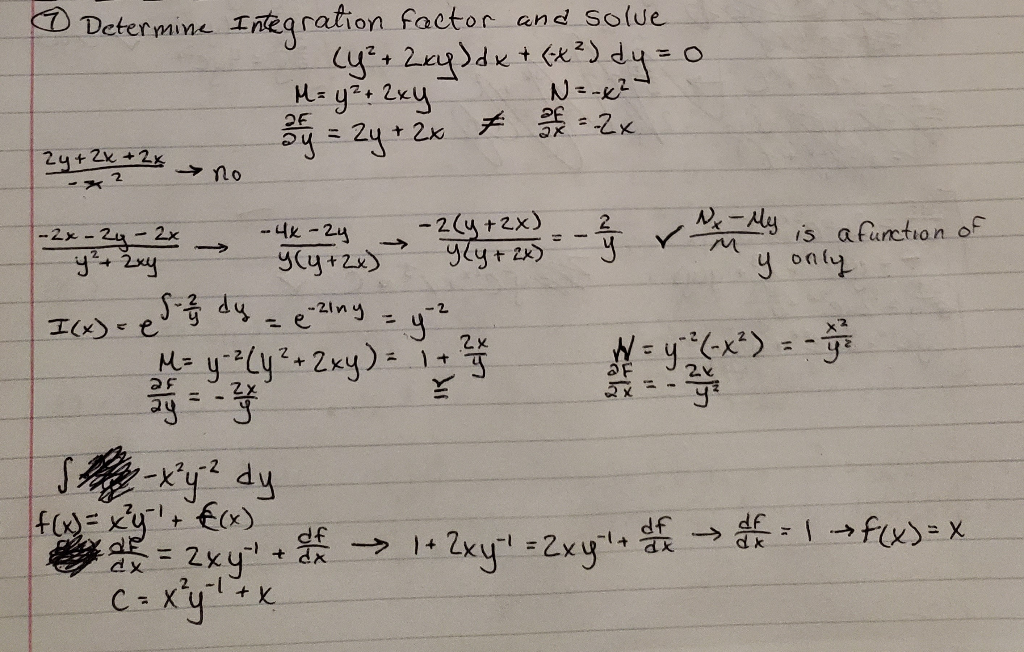



Determine An Integrating Factor For The Given Chegg Com



Q Tbn And9gct0h2o5pe0g19uo6sect5yeyoajck8dueg8x9euzd6dopmlxj4i Usqp Cau



Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf



Solve The Following Differential Equation X 2 Y 2 Dx 2xy Dy 0 Given That Y 1 When X 1 Sarthaks Econnect Largest Online Education Community




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download
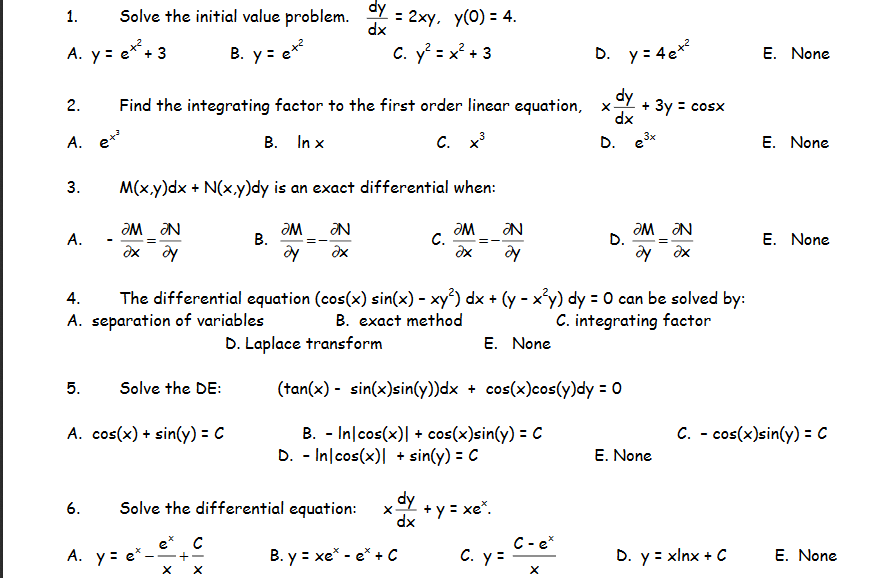



Solve The Initial Value Problem Dy Dx 2xy Y 0 Chegg Com




Solve The Differential Equation X 2 Y 2 Dx 2xydy 0 Youtube




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




2xy Dy Dx X 2 3y 2 Youtube




How To Solve 3xy Y 2 Dx X 2 Xy Dy 0 Also I Wish To Knw When To Use Y Vx Or X Vy Mathematics Topperlearning Com H9faf2xx



X Y 2 Y 2 Dx X 2 X 2 Y Dy 0 How Do You Solve The Differential Equation Quora




Answered Determine The Differential Equation Bartleby




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top



How To Integrate X Y 2 Dx 2xy X 2 Y Dy 0 Quora



ダウンロード X 2 2xy Y 2 Dx X Y 2 Dy 0




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




Solve The Differential Equation And Use Matlab To Plot The Solution 2 Dy 2xy F X Y 0 2 Dx F X X0sx 1 L Homeworklib




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top



What Is The Solution Of X Y 2 Dx 2xydy 0 Quora




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community



Www Tau Ac Il Levant Ode Solution 6 Pdf



Find The Equation Of A Curve Passing Through Origin And Satisfying The Differential Equation 1 X 2dy Dx 2xy 4x2 Studyrankersonline



0 件のコメント:
コメントを投稿