算数への関心・意欲・態度 角柱や円柱の体積の求め方に関心をもち、進んで調べようとする。 数学的な考え方 角柱や円柱の体積の求め方を既習の立体の体積の求め方に帰着して考え, 説明することができる。 数量や図形についての 技能方 1 三角柱の体積を計算で求める方法を 理解する。 既習の立体の体積の求め方を手がかりに、角 柱の体積の求め方を見直す。 *底面が直角三角形の三角柱の体積も、底面積 ×高さで求められることを考える。 2 一般の角柱の体積の公式をまとめ る。小学 算数 複雑な立体の体積の求め方 L字

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
台形 立体 体積 求め方
台形 立体 体積 求め方-このことを用いると,上の図1において, 正方形の面積は,2×2=4(cm2)で, 重心(対角線の交点)がえがく円周の長さは,2π×1=2π(cm)なので, この正方形を回転させてできる立体の体積は, 4×2π=8π(cm3)と求めることができます。小学5年生の算数立体の体積の求め方練習プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
・立方体,直角柱の体積の求め方 6年生 ・角柱,円柱の体積の求め方 表1 表1を見ると,平面図形の四角形の学習では, はじめに,辺が垂直に交わる正方形や長方形を学 習する。次に,辺が直交しない四角形として平行 四辺形を学習している。立体において本単元で扱う立体の体積の求め方は,学習指導要領には以下のように位置づけられている。 第6学年 b 量と測定 (3)図形の体積を計算によって求めることができるようにする。 ア 角柱および円柱の体積の求め方を考えること。それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3)
17/3/ $$ \mbox{水の中に入れた立体の体積} = \mbox{押し出された水の体積} $$ という関係で使う場合もあります。 (練習問題6がそう)Hello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。7 立体の体積と表面積 学基本学習の基本 37 切断と体積⑴ 問題 右の図は ,ab = 6 cmad ae 3 の直方体で ある。辺 ad の中点を m ,辺 bc の中点を n とし,この直方体を 次の平面で切るとき,頂点 a をふくむ方の立体の体積を求めよ。 ⑴ 3 点 m ,n,e を通る平面
6年算数 立体の体積 その1 子どもの学習支援 by いっちに算数 スマホ版 立方体 直方体 6年生は、上の図のように5年生で勉強した「直方体や立方体」の体積の求め方を生かして、下の図のような「三角柱などの角柱や円柱」の体積の求め方を勉強します。体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして
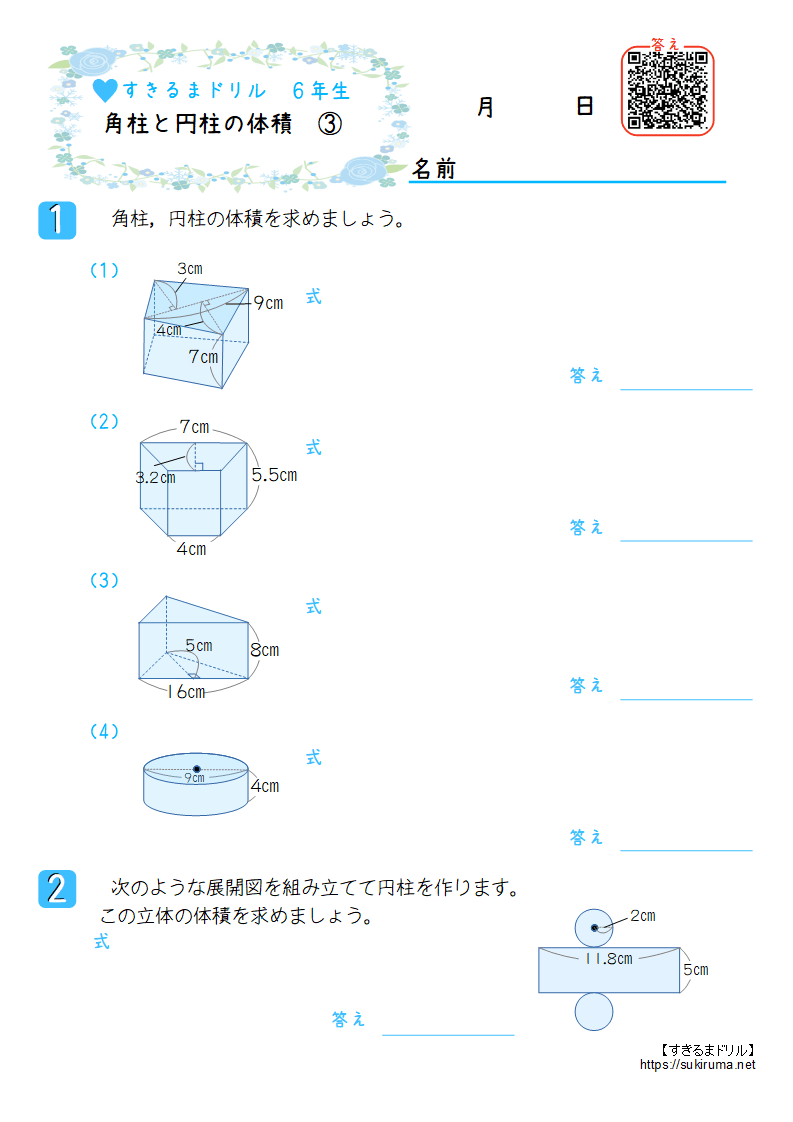



すきるまドリル 小学6年生 算数 角柱と円柱の体積 無料学習プリント すきるまドリル 無料学習プリント




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
立体の体積 体積ボタン 解説 体積ボタン2 解説 立体(L字型) 解説 6年 分数のかけ算とわり算 解説 図形・円と直線の関係 解説 比例 解説 比例と反比例① 解説 比例と反比例① v2 解説 比例と反比例② 解説 変化する2つの量 解説 割合を使ってV=Sh 特に,円柱については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから V=πr 2 h と書くこともできます. ※簡単なことのように見えますが,底面と高さとが直角になっている場合だけこの公式が使えます.例えば,右図において Sl はこの立体の体積ではありません. 要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それ・第5学年で学習した直方体や立方体の求め方を基にして,四角 柱や三角柱の体積を求めるために,第5学年の教科書を振り返 る。 2 3 四角柱(直方体)の体積の 求め方を「底面積×高さ」と 見直し,底面が直角三角形の 三角柱の体積の求め方も同様




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
ア 角柱及び円柱の体積の求め方を考えること。 立体については,第4学年で直方体・立方体を学習したのに続き,第5学年では角柱,円 柱を学習し,直方体・立方体も角柱の仲間であることを学習してきている。立体の体積につ2つ合わせて直方体にして考える 6×5×(6+2)÷2=120 答え( 120㎤ )立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)




小5 算数 小5 3 直方体と立方体の体積 Youtube
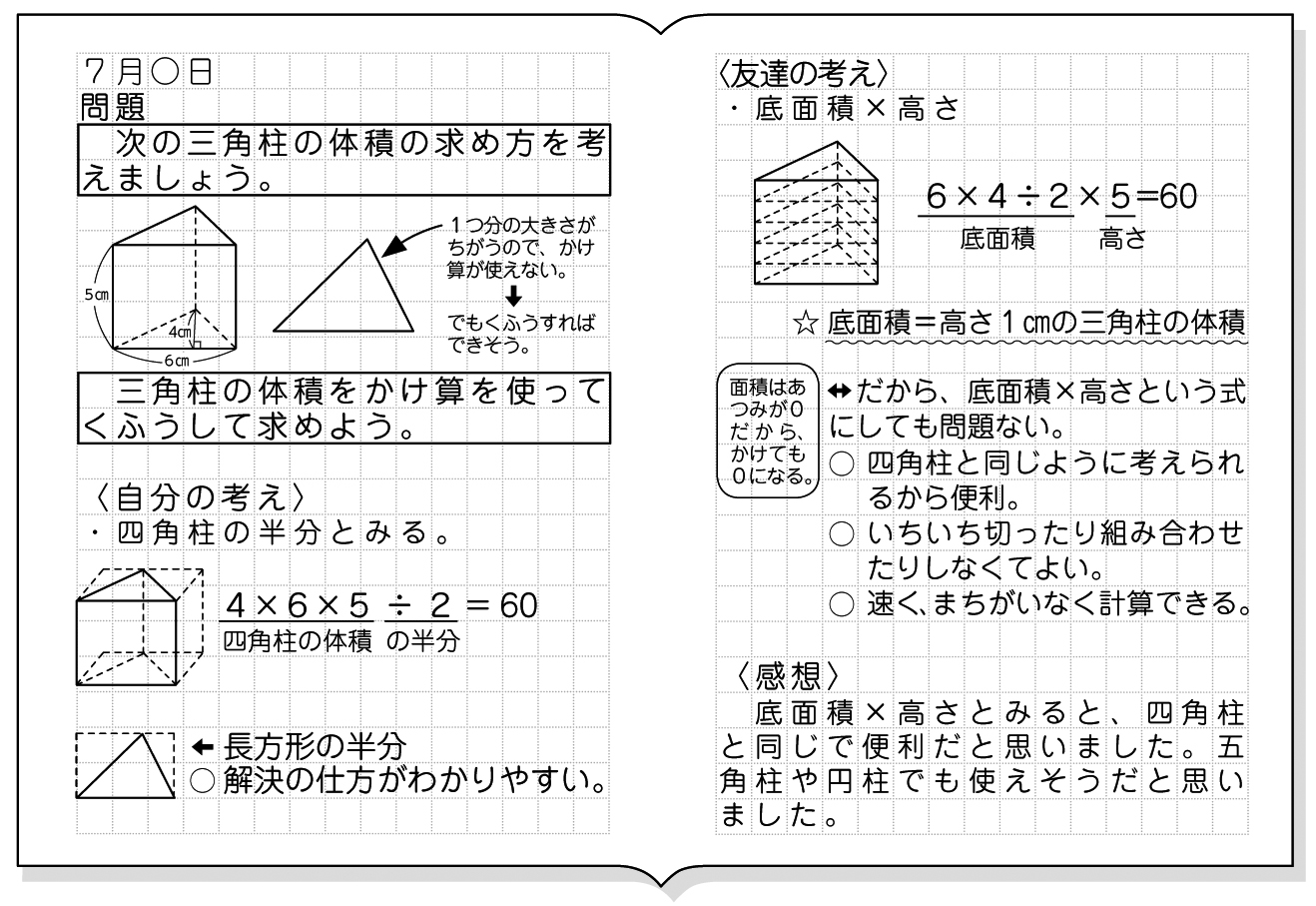



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術
立方体の体積 立方体の体積 立方体の辺の長さから体積と表面積を計算します。 立方体の辺の長さ 立方体の辺の長さ 立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、 落ち着いて計算してみよう!直方体の体積=縦×横×高さで計算します。 立方体は全ての辺の長さが等しいので、立方体の1辺をaとするとき 立方体の体積=a×a×a=a 3




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館
今回は 「立体の体積」 を求めるよ。 体積の求め方は、「すい」と「柱」に関して2つの公式を覚えてしまおう。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




体積の求め方 計算公式一覧
体積 = 底面積 × 高さ19/2/21 定積分で体積を求める ある曲線下の面積を定積分で求められたように、ある平面を積み重ねてできる立体の体積も、定積分で求められます。 このとき、平面の積み重ね方には大きく分けて次の \(2\) 通りがあります。Lesson 43 立体の体積 第6章 空間図形 1 右図の四角柱の体積を求め 家庭教師のガンバは、勉強が嫌いな子、勉強が苦手な子、勉強のやり方がわからない子を中心に年以上運営されている家庭教師センターです。
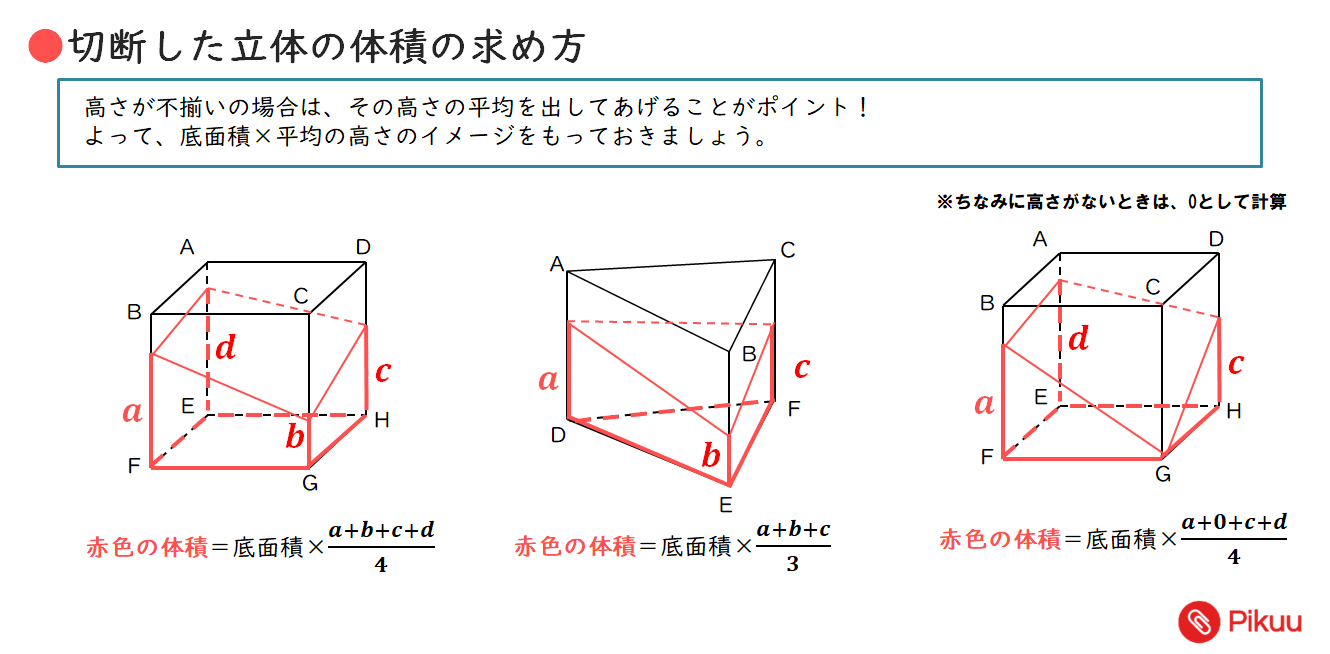



高校入試対策数学 知って得 中学数学の公式テクニック集 Pikuu




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求めるめ× 立体の体積の求め方を説明しよう。 別紙プリント 高さ 2つのキーワードを使って説明しよう! ま 底面と高さを見付け,立体の体積の求め を説明することができる。 ・身の回りの箱の体積を求め,求め方を説明することができた。 《立体の体積の求め方》 求める立体は①と②があわさって出来た立体であることから、①の直方体の体積+②の立方体の体積で求めることが出来ます。 ①の直方体の体積=8×8×4=256(cm³) ②の立方体の体積=4×4×4=64(cm³)



6年算数立体の体積1 教え方



三角錐の体積の求め方 下の図は立方体から三角錐を切り取った立 Yahoo 知恵袋
立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答立体の体積の求め方を、イメージと共に式で捉える。 T:底面の面積と、高さ1㎝の四角柱との体積を比べてみましょう 。 S:底面の面積は縦×横で求め、高さを掛けると体積になるが、高さが1㎝ 答え)体積26 cm 3 表面積cm 2 積み重ねられた立体の表面積:(前+右+上)×2 積み重ねられた立体①:表面積と体積! 答え)体積640cm 3 表面積480cm 2 上記のようにある程度、自分の頭で「投影図→見取り図」が




体積の求め方 計算公式一覧
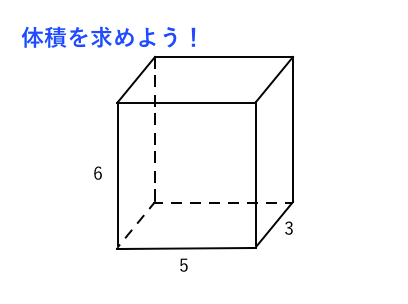



超簡単 体積の求め方 苦手な数学を簡単に



三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




円錐の体積ってなんであの公式なの Webty Staff Blog




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




小5 算数 小5 5 体積の求め方のくふう Youtube




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



5 5 複雑な立体の表面積と面積を求めるには さんすうがく




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
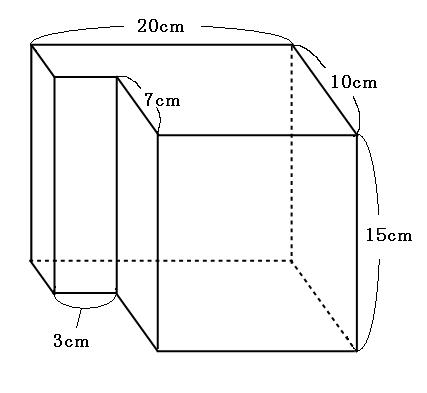



立体の体積の求め方 何角柱でも何角錐でも同じ




円柱の体積の求め方 公式 小学生 中学生の勉強




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
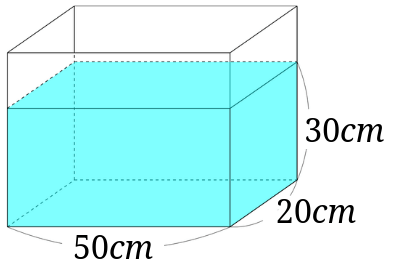



石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




小5 複雑な立体の体積 直方体 日本語版 Youtube




小6 算数 立体の体積 小学生 算数のノート Clear



1
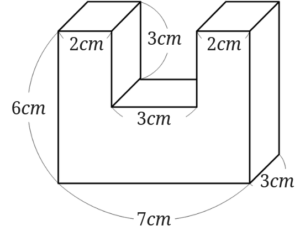



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校



Studydoctor円錐や角錐の体積の求め方 中学1年数学 Studydoctor




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
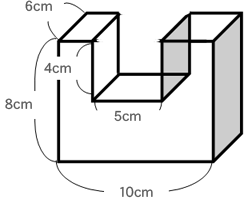



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



立派な 台形 体積 求め 方



Q Tbn And9gcqbxowgsr9fglz9s6nk3xfp1u T2gn5wllytdkpbbfnrgtv43gf Usqp Cau




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




角柱の体積 Youtube



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋
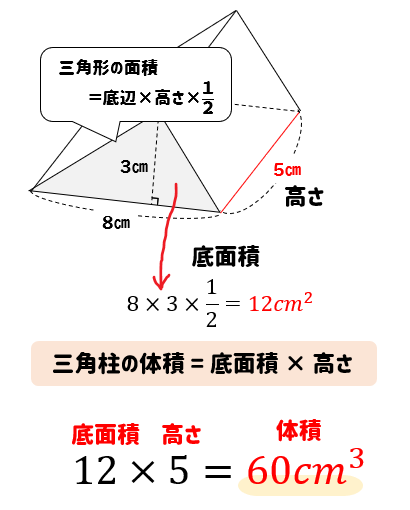



3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




体積の求め方 公式一覧 小学生 中学生の勉強




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




6年の 立体の体積 のソフトが もう1本できました さくら社




丸棒の重量 円柱の体積と重量の求め方 鉄の場合



1




体積の求め方 計算公式一覧
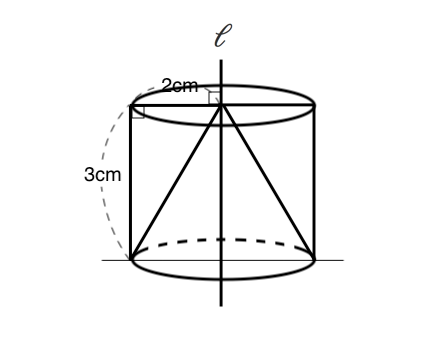



立体の体積を求める問題 回転させてできる立体 苦手な数学を簡単に



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




四角錐台の体積 高精度計算サイト




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




体積比の求め方が分かりません Clear




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



5年算数体積2わかる教え方




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




体積 表面積




中1 数学 中1 立体の体積 Youtube
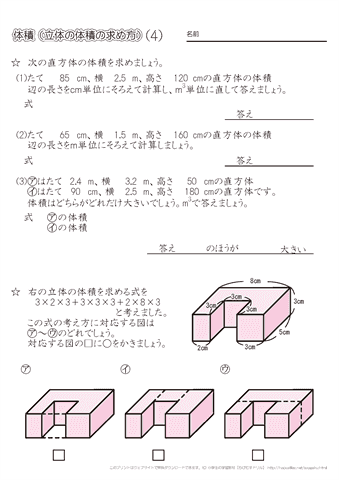



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




どうして1 3なの 錐の体積の公式の求め方 まなべーと




体積の求め方 計算公式一覧



1




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




角錐 円錐の体積と表面積の公式 数学fun



体積の応用




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



6年算数立体の体積その2 教え方
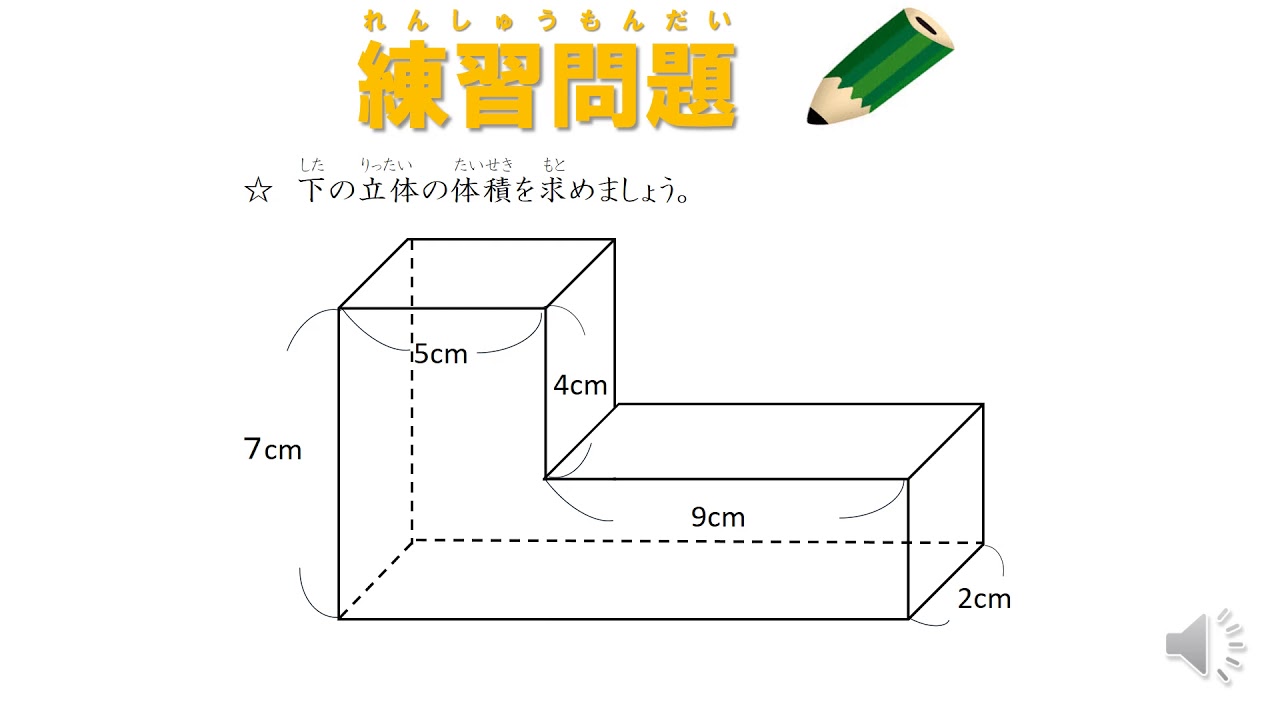



小5 直方体の体積 複雑な立体を求める 日本語版 Youtube




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



算数流体積の求め方 Sciencelab 冨田塾




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積




体積の求め方 計算公式一覧



立体の体積 テストの前に
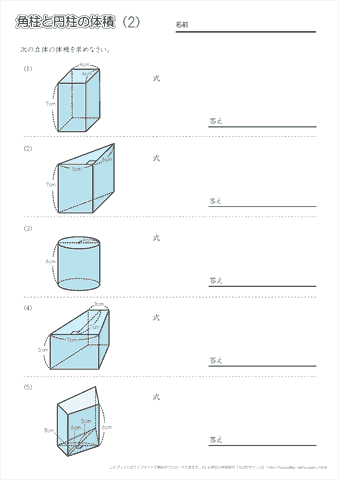



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




公式を図解 すい体の体積 円すいの表面積の求め方



地図の体積計測
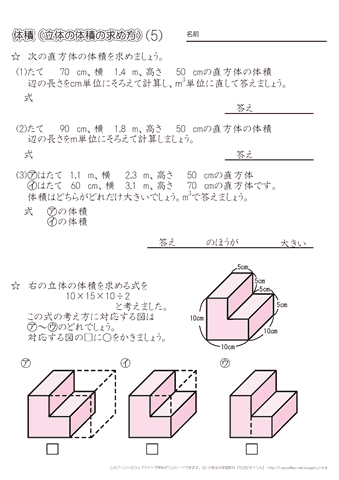



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
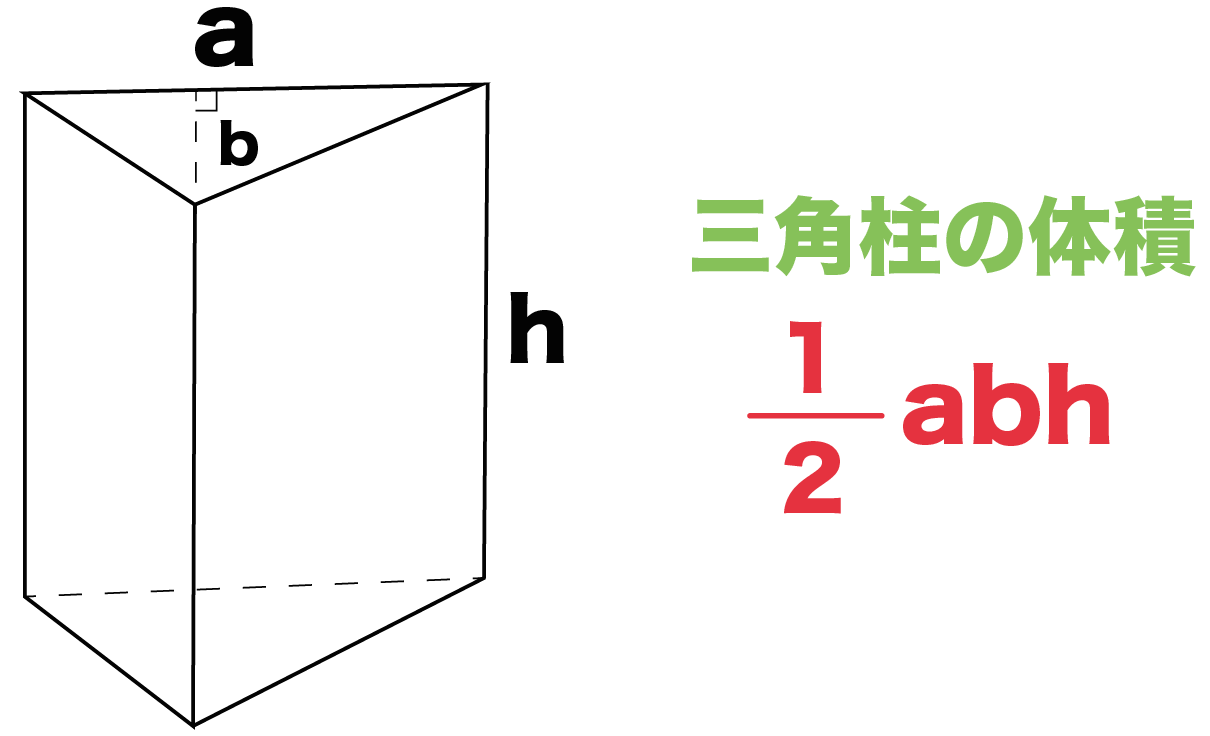



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




立体の体積を求める公式



一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




6年算数立体の体積1 教え方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
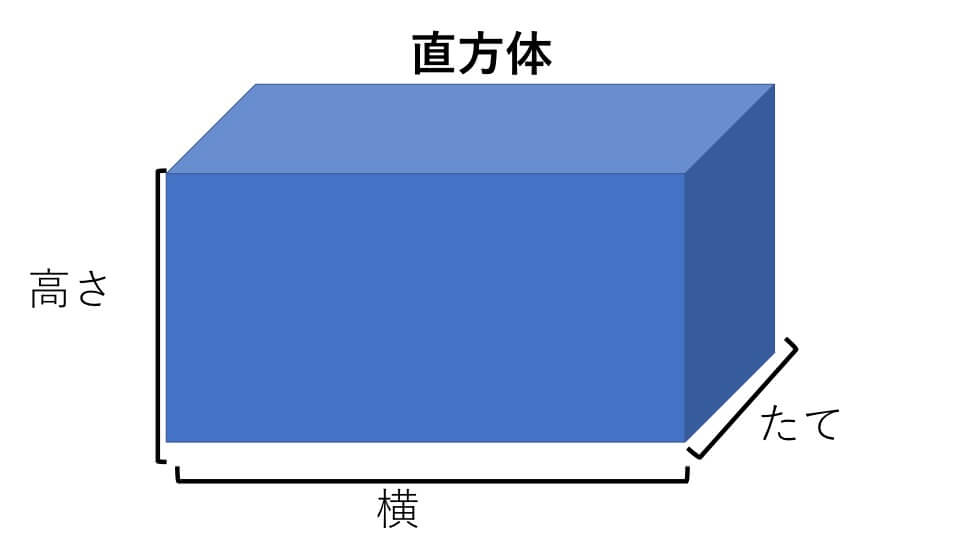



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿